
【题目】为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资30 000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.
(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?
(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20 000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a%(其中![]() ).则每户平均集资的资金在150元的基础上减少了
).则每户平均集资的资金在150元的基础上减少了![]() %,求a的值.
%,求a的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
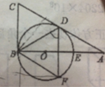
【题目】如图,Rt△ABC中,∠ABC=900,AC=2BC=![]() ,点O在边AB上,以点O为圆心,,OB的长为半径的圆恰好与AC相切于D,与边AB相交于点E.
,点O在边AB上,以点O为圆心,,OB的长为半径的圆恰好与AC相切于D,与边AB相交于点E.
(1)求证:点D为AC的中点;
(2)若点F为半圆BEF上的动点,连接BD、BF、DF,填空:
当∠BDF= 时,四边形BCDF为菱形;
当△BDF为直角三角形时,BF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
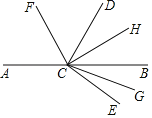
【题目】阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余 ②∠FCG与∠HCG互补 ③∠ECF与∠GCH互补 ④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
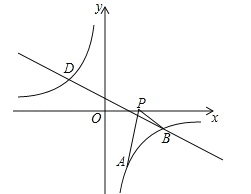
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
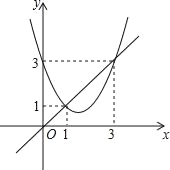
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
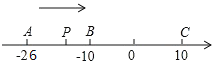
【题目】已知数轴上有A、B、C三点,分别表示有理数﹣26,﹣10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒。
(1)用含t的代数式表示P到点A和点C的距离:PA=_____,PC=_____.
(2)当点P运动到B点时,点Q从A出发,以每秒3个单位的速度向右运动,求t等于多少秒时P、Q两点相遇?t等于多少秒时P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两点在同一条数轴上,点A在原点的左边,到原点的距离为4,点B在原点右边,点A 到B点的距离为16.
(1)求A,B两点所表示的数:
(2)若A,B两点分别以每秒1个单位长度和3个单位长度的速度同时相向移动,在点C相遇,求点C表示的数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中如图所示,
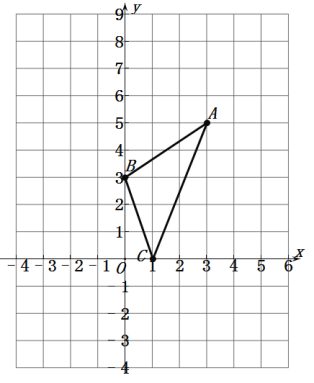
(1)S△ABC= .
(2)x轴上是否存在点P,使得S△BCP=2S△ABC,若不存在,说明理由;若存在,求出P点的坐标.
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
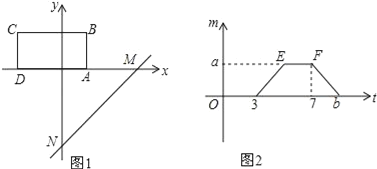
【题目】如图,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2,直线MN:y=x﹣4沿x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图2所示.
(1)点A的坐标为 ,矩形ABCD的面积为 ;
(2)求a,b的值;
(3)在平移过程中,求直线MN扫过矩形ABCD的面积S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com