
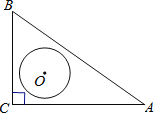
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1 B.1≤r≤![]() C.1≤r≤
C.1≤r≤![]() D.1≤r≤4
D.1≤r≤4
【答案】C
【解析】
试题分析:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,根据题意得出四边形OECF是正方形,得出OF=CF,由勾股定理得出AB=![]() =5,由内心的性质得出CF=OF=1,AF=AC﹣CF=3,由勾股定理求出OA,由直线与圆的位置关系,即可得出结果.
=5,由内心的性质得出CF=OF=1,AF=AC﹣CF=3,由勾股定理求出OA,由直线与圆的位置关系,即可得出结果.
解:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连接OA、OB,如图所示

则四边形OECF是正方形,
∴OF=CF=OE=CE,
∵∠C=90°,AC=4,BC=3,
∴AB=![]() =5,
=5,
∵O是△ABC的内心,
∴CE=CF=OF=OE=![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∴AF=AC﹣CF=3,BE=BC﹣CE=2,
∴OA=![]() =
=![]() =
=![]() ,OB=
,OB=![]() =
=![]() =
=![]() ,
,
当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当1<r≤![]() 时,以O为圆心,r为半径的圆与线段AB有两个交点;
时,以O为圆心,r为半径的圆与线段AB有两个交点;
当![]() <r≤
<r≤![]() 时,以O为圆心,r为半径的圆与线段AB有1个交点;
时,以O为圆心,r为半径的圆与线段AB有1个交点;
∴以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是1≤r≤![]() ;
;
故选:C.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.

(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
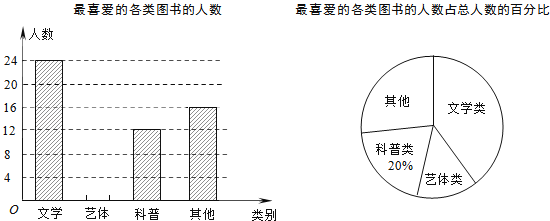
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于距发射架底部4km处的地面雷达站R(LR=4)测得火箭底部的仰角为43°.1s后,火箭到达B点,此时测得火箭底部的仰角为45.72°.这枚火箭从A到B的平均速度是多少 (结果取小数点后两位)?
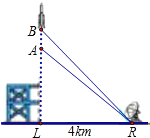
(参考数据:sin43°≈0.682,cos43°≈0.731,tan43°≈0.933,
sin45.72°≈0.716,cos45.72°≈0.698,tan45.72°≈1.025)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2= ;
(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为 ;
(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系: ;
(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com