
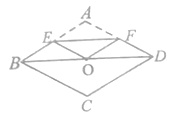
【题目】如图,将边长为4的菱形![]() 纸片折叠,使点
纸片折叠,使点![]() 恰好落在对角线的交点
恰好落在对角线的交点![]() 处,若折痕
处,若折痕![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
【答案】A.
【解析】
试题分析:连接AC,根据菱形的性质得出AC⊥BD,根据折叠得出EF⊥AC,EF平分AO,得出EF∥BD,得出EF为△ABD的中位线,根据三角形中位线定理求出BD的长,进而可得到BO的长,由勾股定理可求出AO的长,则∠ABO可求出,继而∠BAO的度数也可求出,再由菱形的性质可得∠A=2∠BAO.
连接AC,
∵四边形ABCD是菱形,∴AC⊥BD,
∵A沿EF折叠与O重合,∴EF⊥AC,EF平分AO,
∵AC⊥BD,∴EF∥BD,∴E、F分别为AB、AD的中点,
∴EF为△ABD的中位线,∴EF=BD,∴BD=2EF=4![]() ,
,
∴BO=2![]() ,∴AO=
,∴AO=![]() =2,∴AO=
=2,∴AO=![]() AB,
AB,
∴∠ABO=30°,∴∠BAO=60°,∴∠BAD=120°.
故选A.



科目:初中数学 来源: 题型:
【题目】在世界环境日到来之际,希望中学开展了“环境与人类生存”主题研讨活动,活动之一是对我们的生存环境进行社会调查,并对学生的调查报告进行评比.初三.(3)班将本班50篇学生调查报告得分进行整理(成绩均为整数),列出了频率分布表,并画出了频率分布直方图(部分)如下:

根据以上信息回答下列问题:
(1)该班90分以上(含90分)的调查报告共有篇;
(2)该班被评为优秀等级(80分及80分以上)的调查报告占%;
(3)补全频率分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是( )
A. (3,3) B. (3,-3) C. (6,-6) D. (3,3)或(6,-6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,设
中,设![]() 的对边分别为
的对边分别为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,会有
,会有![]() ,则
,则

![]() ,即
,即![]()
同理![]() ,
,![]()
通过推理还可以得到另一个表达三角形边角关系的定理—余弦定理:

在![]() 中,若
中,若![]() 的对边分别为
的对边分别为![]() ,则
,则
![]()
![]()
![]()
用上面的三角形面积公式和余弦定理解决问题:
(1)如图,在![]() 中,
中,![]() ,
,![]() 的对边分别是3和8.
的对边分别是3和8.

求![]() 和
和![]() .
.
解:![]() _______________;
_______________;
![]() ______________.
______________.
(2)在![]() 中,已知
中,已知![]() ,
,![]() 分别是以
分别是以![]() 为边长的等边三角形,设
为边长的等边三角形,设![]() 的面积分别为
的面积分别为![]() ,求证:
,求证: ![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com