
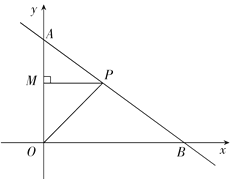
【题目】如图:一次函数![]() 的图象与坐标轴交于A、B两点,点P是函数
的图象与坐标轴交于A、B两点,点P是函数![]() (0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(1)当AP为何值时,△OPM的面积最大?并求出最大值;
(2)当△BOP为等腰三角形时,试确定点P的坐标.
【答案】(1)AP=![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,
,![]() )或(2,
)或(2,![]() ).
).
【解析】
(1)令P点坐标为(x0,y0),根据三角形面积公式列出S△OPM关于x0的二次函数解析式,确定最大值,进而根据相似比求出当△OPM面积最大时AP的长即可;(2)将情况分为BO=BP以及OP=BP两种进行讨论:①当BO=BP时,根据三角形相似求出MP的长,即P点的横坐标,将P点横坐标代入一次函数解析式,即可得到P点的坐标;②当OP=BP时,如图,过点P作PM⊥OB于点N,根据等腰三角形的性质得到ON=![]() OB,ON的长即为P点的横坐标,将ON=2代入一次函数解析式中即可求出P点的纵坐标.
OB,ON的长即为P点的横坐标,将ON=2代入一次函数解析式中即可求出P点的纵坐标.
(1)令点![]() 的坐标为
的坐标为![]() ,
,![]()
![]() 轴,
轴,![]()
将![]() 代入得
代入得![]()
![]() 当
当![]() 时,
时,![]() 的面积,有最大值
的面积,有最大值![]() ,
,
即:![]() ,
,
![]() ,
,
![]()
![]()
即![]()
![]() 直线
直线![]() 分别交两坐标轴于点
分别交两坐标轴于点![]() 、
、![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
(2)①在![]() 中,当
中,当![]() 时
时
![]() ,
,![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
将![]() 代入代入
代入代入![]() 中,得
中,得![]()
![]() ,
,![]() ;
;
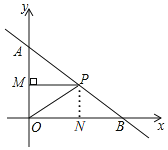
②在![]() 中,当
中,当![]() 时,如图,
时,如图,
过点![]() 作
作![]() 于点
于点![]()
![]() ,
,
![]()
将![]() 代入
代入![]() 中得,
中得,![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
即:点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
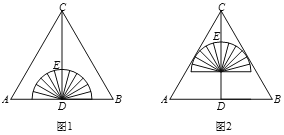
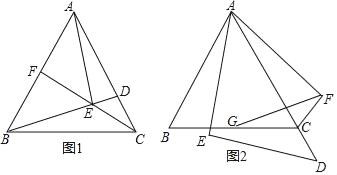
【题目】如图1,将一个量角器与一张等边三角形(△ABC)纸片放置成轴对称图形,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,此时,测得顶点C到量角器最高点的距离CE=2cm,将量角器沿DC方向平移1cm,半圆(量角器)恰与△ABC的边AC,BC相切,如图2,则AB的长为__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m.
(1)若养鸡场面积为200m2,求鸡场靠墙的一边长.
(2)养鸡场面积能达到250m2吗?如果能,请给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D是AC边上一点,连接BD,过点A作AE⊥BD于E.
(1)如图1,连接CE并延长CE交AB于点F,若∠CBD=15°,AB=4,求CE的长;
(2)如图2,当点D在线段AC的延长线上时,将线段AE绕点A逆时针旋转60°得到线段AF,连接EF,交BC于G,连接CF,求证:BG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
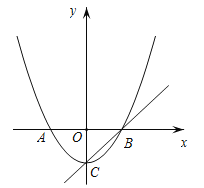
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 过顶点
过顶点![]() 和点
和点![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的解析式;
的解析式;
(3)抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小华和小夏玩掷骰子游戏,他们约定:他们用同一枚质地均匀的骰子各掷一次, 如果两次掷的骰子的点数相同则小华获胜:如果两次掷的骰子的点数的和是6则小夏获胜.
(1)请您列表或画树状图列举出所有可能出现的结果;
(2)请你判断这个游戏对他们是否公平并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
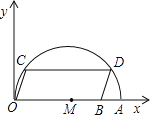
【题目】如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: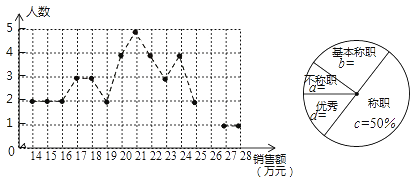
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com