
ĄŸÌâÄżĄżÒŃÖȘŁșÈçÍŒŁŹĆŚÎïÏßy=ax2+bx+cÓëxÖ᜻ÓÚÁœžöȻ͏”Ä”ăAŁš©4ŁŹ0Ł©ŁŹBŁš1ŁŹ0Ł©ŁŹÓëyÖáŐę°ëÖ᜻ÓÚ”ăCŁŹtanĄÏCAB= ![]() Łź
Łź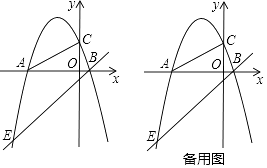
Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœČąŃéÖ€”ăQŁš©1ŁŹ3Ł©ÊÇ·ńÔÚĆŚÎïÏßÉÏŁ»
Łš2Ł©”ăMÊÇÏ߶ÎACÉÏÒ»¶Ż”㣚ȻÓëAŁŹCÖŰșÏŁ©ŁŹčę”ăMŚśxÖá”ÄŽčÏߣŹŽčŚăÎȘHŁŹœ»ĆŚÎïÏßÓÚ”ăNŁŹÊÔĆĐ¶Ï”±MNÎȘŚîŽó֔ʱŁŹÒÔMNÎȘÖ±Ÿ¶”ÄÔČÓëyÖá”ÄλÖĂčŰÏ”ČąË”ĂśÀíÓÉŁ»
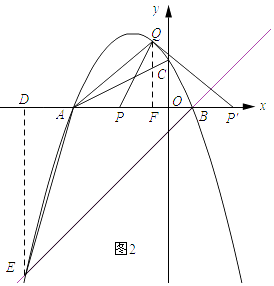
Łš3Ł©ÒŃÖȘčę”ăB”ÄÖ±Ïßy=x©1œ»ĆŚÎïÏßÓÚÁíÒ»”ăEŁŹÎÊŁșÔÚxÖáÉÏÊÇ·ńŽæÔÚ”ăPŁŹÊčÒÔ”ăPŁŹAŁŹQÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜AEBÏàËÆŁżÈôŽæÔÚŁŹÇëÇółöËùÓĐ·ûșÏÒȘÇó”Ä”ăP”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
ĄŸŽđ°žĄż
Łš1Ł©
œâŁșÔÚRtĄśAOCÖĐŁŹĄÏCOA=90ĄăŁŹAO=4ŁŹtanĄÏCAB= ![]() ŁŹ
ŁŹ
ĄàOC=2Łź
ĄàCŁš0ŁŹ2Ł©Łź
ÉèĆŚÎïÏߔĜâÎöÊœÎȘy=aŁšx+4Ł©Łšx©1Ł©ŁŹœ«”ăC”ÄŚű±êŽúÈë”ĂŁș©4a=2ŁŹœâ”Ăa=© ![]() ŁŹ
ŁŹ
ĄàĆŚÎïÏߔĜâÎöÊœÎȘy=© ![]() ĄÁŁšx2+3x©4Ł©ŁŹŒŽy=©
ĄÁŁšx2+3x©4Ł©ŁŹŒŽy=© ![]() x2©
x2© ![]() x+2Łź
x+2Łź
”±x=1ʱŁŹy=© ![]() ĄÁŁš©1Ł©2©
ĄÁŁš©1Ł©2© ![]() ĄÁŁš©1Ł©+2=3Łź
ĄÁŁš©1Ł©+2=3Łź
Ąà”ăQŁš©1ŁŹ3Ł©ÔÚĆŚÎïÏßÉÏ
Łš2Ł©
œâŁșÈçÍŒ1ËùÊŸŁș
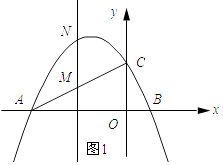
ÉèÖ±ÏßAC”ÄœâÎöÊœÎȘy=kx+bŁŹœ«”ăAĄąC”ÄŚű±êŽúÈë”ĂŁș ![]() ŁŹ
ŁŹ
œâ”ĂŁșk= ![]() ŁŹb=2Łź
ŁŹb=2Łź
ĄàÖ±ÏßAC”ÄœâÎöÊœÎȘy= ![]() x+2Łź
x+2Łź
Éè”ăM”ÄŚű±êÎȘŁšmŁŹ ![]() m+2Ł©ŁŹÔò”ăNŁšmŁŹ©
m+2Ł©ŁŹÔò”ăNŁšmŁŹ© ![]() m2©
m2© ![]() m+2Ł©Łź
m+2Ł©Łź
ĄàMN=© ![]() m2©
m2© ![]() m+2©Łš
m+2©Łš ![]() m+2Ł©=©
m+2Ł©=© ![]() Łšm+2Ł©2+2Łź
Łšm+2Ł©2+2Łź
Ąà”±m=©2ʱŁŹMN”ÄŚîŽóÖ”ÎȘ2Łź
ĄàÒÔMNÎȘÖ±Ÿ¶”ÄÔČ”Ä°ëŸ¶ÎȘ1Łź
ÓÖĄßÒÔMNÎȘÖ±Ÿ¶”ÄÔČ”ÄÔČĐÄ”œyÖá”ÄŸàÀëÎȘ2ŁŹ
ĄàÒÔMNÎȘÖ±Ÿ¶”ÄÔČÓëyÖáÏàÀë
Łš3Ł©
œâŁșÈçÍŒ2ËùÊŸŁșčę”ăEŚśEDĄÍxÖᣏŽčŚăÎȘDŁŹčę”ăQŚśQFĄÍxÖᣏŽčŚăÎȘFŁź
œ«y=x©1Óëy=© ![]() x2©
x2© ![]() x+2ÁȘÁąŁŹœâ”ĂŁșx=©6ŁŹy=©7»òx=1ŁŹy=0ŁŹ
x+2ÁȘÁąŁŹœâ”ĂŁșx=©6ŁŹy=©7»òx=1ŁŹy=0ŁŹ
Ąà”ăE”ÄŚű±êÎȘŁš©6ŁŹ©7Ł©Łź
ĄàBD=ED=7Łź
Ó֥ߥÏEDB=90Ąă
ĄàĄÏEBD=45ĄăŁź
ÍŹÀíĄÏQAF=45ĄăŁź
ĄàĄÏEBD=ĄÏQAF=45ĄăŁź
ĄàĄÏQAD=135ĄăŁŹ90ĄăŁŒĄÏEABŁŒ135ĄăŁź
Ąà”ăPÖ»ÄÜÔÚ”ăA”ÄÓÒČàŁź
ÒÀŸĘÁœ”ăŒä”ÄŸàÀëč«ÊœżÉÖȘŁșEB=7 ![]() ŁŹAQ=3
ŁŹAQ=3 ![]() ŁŹAB=5Łź
ŁŹAB=5Łź
”±ĄśQAPĄäĄŚĄśABEʱŁŹÔò ![]() ŁŹŒŽ
ŁŹŒŽ ![]() =
= ![]() ŁŹœâ”ĂAPĄä=
ŁŹœâ”ĂAPĄä= ![]() ŁŹ
ŁŹ
ĄàOPĄä= ![]() ©4=
©4= ![]() Łź
Łź
”±ŁŹĄśAQPĄŚĄśBEAʱŁŹÔò ![]() ŁŹŒŽ
ŁŹŒŽ ![]() ŁŹœâ”ĂŁșAP=
ŁŹœâ”ĂŁșAP= ![]() ŁŹ
ŁŹ
ĄàOP=5© ![]() =
= ![]() Łź
Łź
Ąà”ăP”ÄŚű±êÎȘŁșŁš ![]() ŁŹ0Ł©»òŁš©
ŁŹ0Ł©»òŁš© ![]() ŁŹ0Ł©
ŁŹ0Ł©
ĄŸœâÎöĄżŁš1Ł©ÒÀŸĘÈńœÇÈęœÇșŻÊę”ĶšÒćżÉÇó”ĂOC=2ŁŹŽÓ¶ű”Ă”œ”ăCŁš0ŁŹ2Ł©ŁŹÉèĆŚÎïÏߔĜâÎöÊœÎȘy=aŁšx+4Ł©Łšx©1Ł©ŁŹœ«”ăC”ÄŚű±êŽúÈëżÉÇó”Ăa”ÄÖ”ŁŹŽÓ¶űżÉ”Ă”œĆŚÎïÏߔĜâÎöÊœŁŹÈ»șóÒÀŸĘ”ăQ”ÄŚű±êÊÇ·ń·ûșÏĆŚÎïÏߔĜâÎöÊœżÉÖȘ”ăQÊÇ·ńÔÚĆŚÎïÏßÉÏŁ»Łš2Ł©ÏÈÇó”ĂÖ±ÏßAC”ÄœâÎöÊœŁŹÉè”ăM”ÄŚű±êÎȘŁšmŁŹ ![]() m+2Ł©ŁŹÔò”ăNŁšmŁŹ©
m+2Ł©ŁŹÔò”ăNŁšmŁŹ© ![]() m2©
m2© ![]() m+2Ł©ŁŹÈ»șóÁĐłöMN”Äł€¶ÈÓëm”ÄșŻÊę”ÄčŰϔʜŁŹÀûÓĂĆä·œ·šżÉÇó”ĂMN”ÄŚîŽóÖ”ÒÔŒ°ŽËʱm”ÄÖ”ŁŹÈ»șóÒÀŸĘdșÍr”ÄčŰÏ”żÉĆжšłöÒÔMNÎȘÖ±Ÿ¶”ÄÔČÓëyÖá”ÄλÖĂčŰÏ”Ł»Łš3Ł©čę”ăEŚśEDĄÍxÖᣏŽčŚăÎȘDŁŹčę”ăQŚśQFĄÍxÖᣏŽčŚăÎȘFŁźÏÈÇó”Ă”ăE”ÄŚű±êŁŹÈ»șóżÉրÜĄśDBEșÍĄśAQFŸùÎȘ”ÈŃüÖ±œÇÈęœÇĐÎŁŹčÊŽËÔÚĄśBAEșÍĄśAQPÖĐŁŹĄÏQAP=ĄÏABEŁŹÈ»șóÒÀŸĘÁœ”ăŒä”ÄŸàÀëč«ÊœÇó”ĂEBĄąAQŁŹAB”Äł€ŁŹÈ»șó·ÖÎȘĄśQAPĄäĄŚĄśABEĄąĄśAQPĄŚĄśBEAÁœÖÖÇéżöÇóœâŒŽżÉŁź
m+2Ł©ŁŹÈ»șóÁĐłöMN”Äł€¶ÈÓëm”ÄșŻÊę”ÄčŰϔʜŁŹÀûÓĂĆä·œ·šżÉÇó”ĂMN”ÄŚîŽóÖ”ÒÔŒ°ŽËʱm”ÄÖ”ŁŹÈ»șóÒÀŸĘdșÍr”ÄčŰÏ”żÉĆжšłöÒÔMNÎȘÖ±Ÿ¶”ÄÔČÓëyÖá”ÄλÖĂčŰÏ”Ł»Łš3Ł©čę”ăEŚśEDĄÍxÖᣏŽčŚăÎȘDŁŹčę”ăQŚśQFĄÍxÖᣏŽčŚăÎȘFŁźÏÈÇó”Ă”ăE”ÄŚű±êŁŹÈ»șóżÉրÜĄśDBEșÍĄśAQFŸùÎȘ”ÈŃüÖ±œÇÈęœÇĐÎŁŹčÊŽËÔÚĄśBAEșÍĄśAQPÖĐŁŹĄÏQAP=ĄÏABEŁŹÈ»șóÒÀŸĘÁœ”ăŒä”ÄŸàÀëč«ÊœÇó”ĂEBĄąAQŁŹAB”Äł€ŁŹÈ»șó·ÖÎȘĄśQAPĄäĄŚĄśABEĄąĄśAQPĄŚĄśBEAÁœÖÖÇéżöÇóœâŒŽżÉŁź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĄśABCÖĐŁŹADÊÇBC±ßÉÏ”ÄžßŁŹAEĄąBF·Ö±đÊÇĄÏBACĄąĄÏABC”ÄÆœ·ÖÏߣŹĄÏBAC=50ĄăŁŹĄÏABC=60ĄăŁŹÔòĄÏEAD+ĄÏACD=ŁšĄĄĄĄŁ©

A. 75Ąă B. 80Ąă C. 85Ąă D. 90Ąă
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĄśABCŸčęÒ»ŽÎÆœÒÆ”œĄśDFE”ÄλÖĂŁŹÇë»ŰŽđÏÂÁĐÎÊÌâŁș
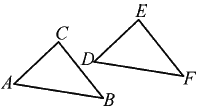
(1)”ăC”ĶÔÓŠ”ăÊÇ”ă__________ŁŹĄÏD=__________ŁŹBC=__________Ł»
(2)ÁŹœÓCEŁŹÄÇĂŽÆœÒƔķœÏòŸÍÊÇ__________”Ä·œÏòŁŹÆœÒƔğàÀëŸÍÊÇÏ߶Î__________”Äł€¶ÈŁ»
(3)ÁŹœÓADŁŹBFŁŹBEŁŹÓëÏ߶ÎCEÏà”È”ÄÏ߶ÎÓĐ__________.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż2017Äê3ÔÂ23ÈŐŁŹÔÚÊÀœç±Ô€ÈüŃÇÖȚÇű12ÇżÈüAŚé6Â֔ĜÏÁżÖĐŁŹÖĐčúŚăÇò¶ÓÒÔ1©0”ıȷÖŐœÊ€À϶ÔÊÖș«čú¶ÓœúŒ¶12ÇżŁźÄłłőÖĐѧУÎȘÁËÁËœâ±ŸĐŁ800ĂûѧÉú¶Ô±ŸŽÎ±ÈÈü”ÄčŰŚąłÌ¶ÈŁŹÒÔ±ăŚöșĂÒę”ŒșÍœÌÓę而śŁŹËæ»úłéÈĄÁË150ĂûѧÉúœűĐĐ”śČ飏°ŽÄꌶÈËÊęșÍčŰŚąłÌ¶ÈŁŹ·Ö±đ»æÖÆÁËÌőĐÎÍłŒÆÍŒŁšÍŒ1Ł©șÍÉÈĐÎÍłŒÆÍŒŁšÍŒ2Ł©Łź 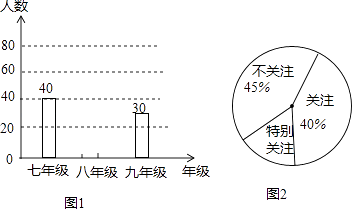
Łš1Ł©ÇëÄăČčÈ«ÌőĐÎÍłŒÆÍŒŁŹČąÇóĄ°Ì۱đčŰŚąĄ±ËùÔÚÉÈĐΔÄÔČĐĜǔĶÈÊꣻ
Łš2Ł©ÇóÈ«ĐŁČ»čŰŚą±ŸłĄ±ÈÈü”ÄѧÉúŽóÔŒÓжàÉÙĂûŁż
Łš3Ł©ÔÚŐâŽÎ”śČéÖĐ ŁŹŸĆÄꌶčČÓĐÁœÎ»ÄĐÉúșÍÁœÎ»ĆźÉúĄ°Č»čŰŚąĄ±±ŸŽÎ±ÈÈüŁŹÏÖŚŒ±žŽÓËÄÈËÖĐËæ»úłéÈĄÁœÈËœűĐĐŚùÌžŁŹÇëÓĂÁĐ±í·š»ò»ÊśŚŽÍŒ”Ä·œ·šÇółöłéÈĄ”ÄÁœÈËÇĄșĂÊÇÒ»ÄĐÉúșÍÒ»ĆźÉú”ÄžĆÂÊŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹ”ăEÎȘŸŰĐÎABCD”ıßBC”ÄÖД㣏ÒÔDEÎȘÖ±Ÿ¶”ÄĄŃOœ»ADÓÚH”㣏čę”ăHŚśHFĄÍAEÓÚ”ăFŁź 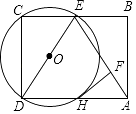
Łš1Ł©ÇóÖ€ŁșHFÊÇĄŃO”ÄÇĐÏߣ»
Łš2Ł©ÈôDH=3ŁŹAF=2ŁŹÇóĄŃO”İ럶Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔĶÁÏÂÁĐČÄÁÏŁș
ÔÚŃ§Ï°Ą°·ÖÊœ·œłÌŒ°Æäœâ·šĄ±čęłÌÖĐŁŹÀÏÊŠÌáłöÒ»žöÎÊÌâŁșÈôčŰÓÚx”Ä·ÖÊœ·œłÌ![]() ”ÄœâÎȘŐęÊ꣏Çóa”ÄÈĄÖ”·¶Î§Łż
”ÄœâÎȘŐęÊ꣏Çóa”ÄÈĄÖ”·¶Î§Łż
ŸčęĐĄŚéœ»ÁśÌÖÂÛșóŁŹÍŹŃ§ĂÇÖđœ„ĐÎłÉÁËÁœÖÖÒâŒûŁș
ХÜ˔ŁșœâŐâžöčŰÓÚx”Ä·ÖÊœ·œłÌŁŹ”Ă”œ·œłÌ”ÄœâÎȘx=a©2ŁźÓÉÌâÒâżÉ”Ăa©2ŁŸ0ŁŹËùÒÔaŁŸ2ŁŹÎÊÌâœâŸöŁź
Хǿ˔ŁșÄăżŒÂÇ”ÄČ»È«ĂæŁź»č±ŰĐ뱣րaĄÙ3ČĆĐĐŁź
ÀÏÊŠË”ŁșĐĄÇżËùË”ÍêÈ«ŐęÈ·Łź
Çë»ŰŽđŁșĐĄĂśżŒÂÇÎÊÌâČ»È«ĂæŁŹÖśÒȘÌćÏÖÔÚÄÄÀïŁżÇëÄăŒòÒȘ˔ÜŁșĄĄ ĄĄŁź
ÍêłÉÏÂÁĐÎÊÌâŁș
Łš1Ł©ÒŃÖȘčŰÓÚx”Ä·œłÌ![]() =1”ÄœâÎȘžșÊ꣏Çóm”ÄÈĄÖ”·¶Î§Ł»
=1”ÄœâÎȘžșÊ꣏Çóm”ÄÈĄÖ”·¶Î§Ł»
Łš2Ł©ÈôčŰÓÚx”Ä·ÖÊœ·œłÌ![]() =©1ÎȚœâŁźÖ±œÓĐŽłön”ÄÈĄÖ”·¶Î§Łź
=©1ÎȚœâŁźÖ±œÓĐŽłön”ÄÈĄÖ”·¶Î§Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒ»ŚéŐę·œĐΰŽÈçÍŒËùÊŸ”Ä·œÊœ·ĆÖĂŁŹÆäÖж„”ăB1ÔÚyÖáÉÏŁŹ¶„”ăC1ĄąE1ĄąE2ĄąC2ĄąE3ĄąE4ĄąC3ĄÔÚxÖáÉÏŁŹÒŃÖȘŐę·œĐÎA1B1C1D1”ı߳€ÎȘ1ŁŹĄÏB1C1O=60ĄăŁŹB1C1ĄÎB2C2ĄÎB3C3ĄŁŹÔòŐę·œĐÎA2017B2017C2017D2017”ı߳€ÊÇŁš Ł© 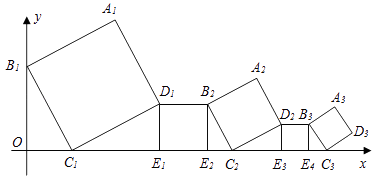
A.Łš ![]() Ł©2016
Ł©2016
B.Łš ![]() Ł©2017
Ł©2017
C.Łš ![]() Ł©2016
Ł©2016
D.Łš ![]() Ł©2017
Ł©2017
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
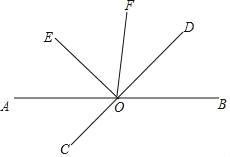
ĄŸÌâÄżĄżÈçÍŒŁŹÖ±ÏßABĄąCDÏàœ»ÓÚ”ăOŁŹOEĄÍODŁŹOEÆœ·ÖĄÏAOFŁź
Łš1Ł©ĄÏBODÓëĄÏDOFÏà”ÈÂđŁżÇë˔ÜÀíÓÉŁź
Łš2Ł©ÈôĄÏDOF=![]() ĄÏBOEŁŹÇóĄÏAOD”ĶÈÊ꣟
ĄÏBOEŁŹÇóĄÏAOD”ĶÈÊ꣟
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÖ±œÇÈęœÇĐÎÖœÆŹ ABC ÖĐŁŹĄÏACBŁœ90ĄăŁŹACĄÜBCŁźÈçÍŒŁŹœ«ÖœÆŹŃŰÄłÌőÖ±ÏßŐÛ”țŁŹÊč”ă A ÂäÔÚÖ±œÇ±ß BC ÉÏŁŹŒÇÂä”ăÎȘ DŁźÉèŐÛșÛÓë ABĄąAC ±ß·Ö±đœ»ÓÚ”ă EĄą”ă FŁŹ”±ŐÛ”țșó”ÄĄśCDF Ó륜BDE ŸùÎȘ”ÈŃüÈęœÇĐÎŁŹÄÇĂŽÖœÆŹÖĐĄÏB ”ĶÈÊęÊÇ_____
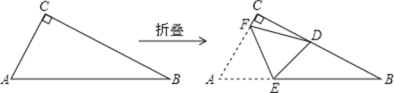
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com