
【题目】如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F. 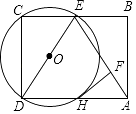
(1)求证:HF是⊙O的切线;
(2)若DH=3,AF=2,求⊙O的半径.
【答案】
(1)证明:连接OH,
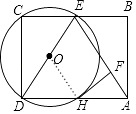
∵四边形ABCD为矩形,
∴CD=BA,∠C=∠B=90°,
∵E是BC的中点,
∴CE=BE,
∴△CDE≌△BAE(SAS),
∴ED=EA,
∴∠EDA=∠EAD,
∵OD=OH,
∴∠EDA=∠OHD,
∴∠EAD=∠OHD,
∴OH∥AE,
∵HF⊥AE,
∴HF⊥OH,
∵点H为⊙O上,OH为⊙O的半径,
∴HF是⊙O的切线
(2)解:连接EH,
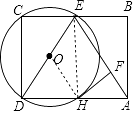
∵DE是⊙O的直径,
∴∠DHE=90°,
∵∠C=∠B=90°,
∴四边形HECD是矩形,
∴CE=DH,
同理:BE=AH,
∵CE=BE,
∴DH=AH=3,
∵CB∥AD,
∴∠BEA=∠EAD,
∵∠HFA=∠B=90°,
∴△FHA∽△BAE,
∴ ![]() ,
,
∴ ![]() ,
,
∴AE= ![]() ,
,
∴OD= ![]() DE=
DE= ![]() AE=
AE= ![]() ×
× ![]() =
= ![]() ,
,
∴⊙O的半径为 ![]() .
.
【解析】(1)连接半径OH,证明HF⊥OH即可;(2)连接EH,证明四边形HECD是矩形,则CE=DH,同理:BE=AH,再证明△FHA∽△BAE,列比例式为: ![]() ,求AE的长,由(1)知:DE=AE,且DE是直径,由此可得半径的长.
,求AE的长,由(1)知:DE=AE,且DE是直径,由此可得半径的长.
【考点精析】根据题目的已知条件,利用矩形的性质和切线的判定定理的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB. 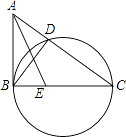
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4,tan∠AEB= ![]() ,AB:BC=2:3,求圆的直径.
,AB:BC=2:3,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=1,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年12月28日举行了微山县南阳镇北、两城镇南跨湖高速的路线开工仪式,其中的一项工程由A、B两工程队合作,120天可以完成;如果A,B两工程队单独完成此项工程,B工程队所用时间是A工程队的1.5倍.
(1)求A,B两工程队单独完成此项工程各需多少天?
(2)在施工过程中,该总公司派一名技术人员在现场对施工质量进行全程监督,每天总公司补助技术人员100元,若由A工程队单独施工,平均每天A工程队的费用为0.5万元,现总公司选择了B工程队单独施工,要求总费用不能超过选择A工程队时的总费用,则平均每天B工程队的费用最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣4,0),B(1,0),与y轴正半轴交于点C,tan∠CAB= ![]() .
.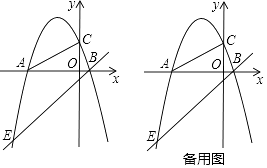
(1)求抛物线的解析式并验证点Q(﹣1,3)是否在抛物线上;
(2)点M是线段AC上一动点(不与A,C重合),过点M作x轴的垂线,垂足为H,交抛物线于点N,试判断当MN为最大值时,以MN为直径的圆与y轴的位置关系并说明理由;
(3)已知过点B的直线y=x﹣1交抛物线于另一点E,问:在x轴上是否存在点P,使以点P,A,Q为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象经过二次函数y=ax2+bx图象的顶点(﹣
的图象经过二次函数y=ax2+bx图象的顶点(﹣ ![]() ,m)(m>0),则有( )
,m)(m>0),则有( ) 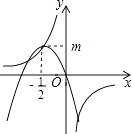
A.a=b+2k
B.a=b﹣2k
C.k<b<0
D.a<k<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x与反比例函数y=
x与反比例函数y= ![]() 在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).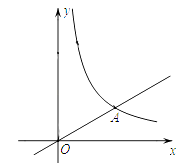
(1)求该反比例函数的关系式;
(2)将直线y= ![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;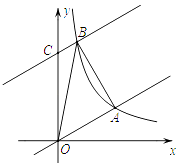
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com