
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
【答案】(1):m<![]() 且m≠﹣
且m≠﹣![]() ;(2)n=1或n=
;(2)n=1或n=![]() .
.
【解析】
考虑分式的分母不为0,即分式必须有意义;
(1)表示出分式方程的解,由解为负数确定出m的范围即可;
(2)分式方程去分母转化为整式方程,根据分式方程无解,得到有增根或整式方程无解,确定出n的范围即可.
请回答:小明没有考虑分式的分母不为0(或分式必须有意义)这个条件;
(1)解关于x的分式方程得,x=![]() ,
,
∵方程有解,且解为负数,
∴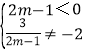 ,
,
解得:m<![]() 且m≠-
且m≠-![]() ;
;
(2)分式方程去分母得:3-2x+nx-2=-x+3,即(n-1)x=2,
由分式方程无解,得到x-3=0,即x=3,
代入整式方程得:n=![]() ;
;
当n-1=0时,整式方程无解,此时n=1,
综上,n=1或n=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
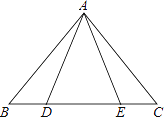
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y= ![]() 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1 , y1)和点(x2 , y2)在反比例函数的图象上,若x1>x2 , 则y1<y2;③不等式x+2<
在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1 , y1)和点(x2 , y2)在反比例函数的图象上,若x1>x2 , 则y1<y2;③不等式x+2< ![]() 的解集是0<x<1.其中正确的有( )
的解集是0<x<1.其中正确的有( ) 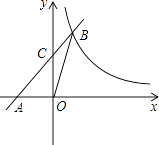
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )

A. 30 B. 50 C. 66 D. 80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣4,0),B(1,0),与y轴正半轴交于点C,tan∠CAB= ![]() .
.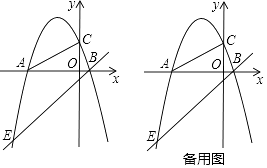
(1)求抛物线的解析式并验证点Q(﹣1,3)是否在抛物线上;
(2)点M是线段AC上一动点(不与A,C重合),过点M作x轴的垂线,垂足为H,交抛物线于点N,试判断当MN为最大值时,以MN为直径的圆与y轴的位置关系并说明理由;
(3)已知过点B的直线y=x﹣1交抛物线于另一点E,问:在x轴上是否存在点P,使以点P,A,Q为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽炫图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽炫图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )
,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,A、B、C分别为数轴上的三点,A点对应的数为-200,B点对应的数为-20,C点对应的数为40.甲从C点出发,以6单位/秒的速度向左运动.
(1)当甲在B点、C点之间运动时,设运时间为x秒,请用x的代数式表示:
甲到A点的距离: ;
甲到B点的距离: ;
甲到C点的距离: .
(2)当甲运动到B点时,乙恰好从A点出发,以4单位/秒的速度向右运动,设两人在数轴上的D点相遇,求D点对应的数;
(3)若当甲运动到B点时,乙恰好从A点出发,以4单位/秒的速度向左运动,设两人在数轴上的E点相遇,求E点对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
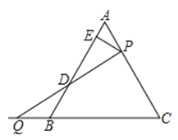
【题目】如图,△ABC 是边长为 6 cm 的等边三角形,P 从点 A 岀发沿 AC 边向 C 运动, 与此同时 Q 从 B 出发以相同的速度沿 CB 延长线方向运动.当 P 到达 C 点时,P、Q 停止运动, 连接 PQ 交 AB 于 D
(1)设 P、Q 的运动速度为 1 cm/s,当运动时间为多少时,∠BQD=30°?
(2)过 P 作 PE⊥AB 于 E,在运动过程中线段 ED 的长是否发生变化?如果不变,求出线段 ED的长;如果变化请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com