Question

【题目】如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E，连接AG.

(1)求证：AG＝CG；

(2)求证：AG2＝GE·GF.

Answer 1

【答案】（1）证明见解析 （2）证明见解析

【解析】试题分析：

（1）由菱形的性质易证△ADG≌△CDG，从而可得AG=CG；

（2）由△ADG≌△CDG可得∠EAG=∠DCG，再由AB∥CD可得∠F=∠DCG，从而可得∠F=∠EAG，再利用∠AGE是公共角可证△AGE∽△FGA就可得到，所以

试题解析：

（1）∵四边形ABCD是菱形，

∴AD＝CD，∠ADB＝∠CDB，

在△ADG与△CDG中， ，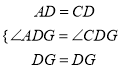

∴△ADG≌△CDG，

∴AG＝CG.

(2) ∵在菱形ABCD中，AB∥CD，

∴∠F＝∠GCD.

∵△ADG≌△CDG，

∴∠EAG＝∠DCG，

∴∠EAG＝∠F.

又∵∠AGE＝∠FGA，

∴△AGE∽△FGA，

∴，

∴AG2＝GE·GF.