
【题目】已知![]() 的半径为
的半径为![]() ,
,![]() 是
是![]() 的弦,点
的弦,点![]() 在
在![]() 上,
上,![]() .若点
.若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() 的度数为______.
的度数为______.
【答案】![]() ,
,![]() 或
或![]()
【解析】
分三种情况:当PC⊥AB交AB延长线上时,当AB垂直平分OP时,当点C在BA延长线上时,利用三角函数,平行四边形的性质分别求出![]() 的度数.
的度数.
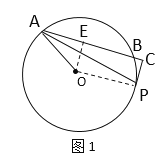
如图1,
当PC⊥AB交AB延长线上时,过点O作OE⊥AB于E,
∵![]() ,
,
∴AE=![]() ,
,
∵OA=2,
∴cos∠OAE=![]() ,
,
∴∠OAE=30°,
∴OE=1,
∵PC=1,OE⊥AB,PC⊥AB,
∴PC=OE,PC∥OE,
∴四边形PCEO是平行四边形,
∴OP∥AC,
∴∠OPA=∠PAB,
∵OA=OP,
∴∠OAP=∠OPA=∠PAB,
∴∠PAB=15°;
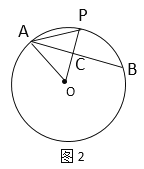
如图2,当AB垂直平分OP时,
∵OP=2,∴PC=1,
∵OA=2,OC=1,
∴∠BAO=30°,
∴∠AOC=60°,
∵OA=OP,
∴∠OAP=∠OPA=60°,
∴AC⊥OP,
∴∠PAB=30°;
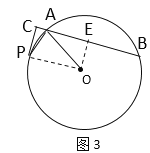
如图3,当点C在BA延长线上时,可知四边形POEC是平行四边形,
∴OP∥AB,
∴∠AOP=∠OAB=30°,
∵OA=OP,
∵∠PAO=75°,
∴∠PAB=∠PAO+∠OAB=105°,
故答案为:![]() ,
,![]() 或
或![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
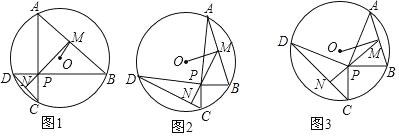
【题目】点P为⊙O内一点,A、B、C、D为圆上顺次四个点,连接AB、CD,OM⊥AB于点M,连接MP并延长交CD于点N,连接PA、PB、PC、PD.
(1)如图1,若A、P、C三点共线,B、P、D三点共线,且AC⊥BD,求证:PN⊥CD;
(2)如图2,若PA=PD,PA⊥PD,PC=PB,PC⊥PB,求证:PN⊥CD;
(3)如图3,在(2)的条件下,PA=10,PC=6,∠APB=60°,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其对称轴为直线
点,其对称轴为直线![]() .
.
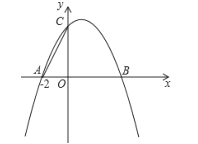
(1)直接写出抛物线的解析式;
(2)把线段![]() 沿
沿![]() 轴向右平移,设平移后
轴向右平移,设平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 落在抛物线上时,求
落在抛物线上时,求![]() 、
、![]() 的坐标;
的坐标;
(3)除(2)中的平行四边形![]() 外,在
外,在![]() 轴和抛物线上是否还分别存在点
轴和抛物线上是否还分别存在点![]() 、
、![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,求出
为顶点的四边形为平行四边形?若存在,求出![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是反比例函数
是反比例函数![]()
![]() 图象上的点,
图象上的点,![]() 于点
于点![]() ,
,![]() .
.
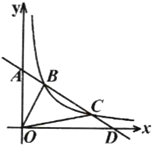
(1)求直线![]() 的函数解析式及反比例函数的解析式;
的函数解析式及反比例函数的解析式;
(2)若![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 的一个数量关系式.
的一个数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 、
、![]() 在第二象限,横坐标分别是-4、-2、-1,双曲线
在第二象限,横坐标分别是-4、-2、-1,双曲线![]() 过
过![]() 、
、![]() 、
、![]() 三点,且
三点,且![]() .
.
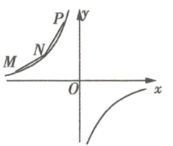
(1)求双曲线的解析式;
(2)过![]() 点的直线
点的直线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,且
,且![]() ,且交
,且交![]() 于另一点
于另一点![]() ,求
,求![]() 点坐标;
点坐标;
(3)以![]() 为边(顺时针方向)作正方形
为边(顺时针方向)作正方形![]() ,平移正方形使
,平移正方形使![]() 落在
落在![]() 轴上,点
轴上,点![]() 、
、![]() 对应的点
对应的点![]() 、
、![]() 正好落在反比例函数
正好落在反比例函数![]() 上,求
上,求![]() 对应点
对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
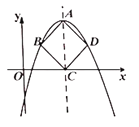
【题目】如图,抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,当以
,当以![]() 为对角线的正方形
为对角线的正方形![]() 的另外两个顶点
的另外两个顶点![]() 、
、![]() 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形
恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形![]() 为它的内接正方形.
为它的内接正方形.
(1)当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;当抛物线
______;当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;
______;
(2)若抛物线![]() 是美丽抛物线时,则请直接写出
是美丽抛物线时,则请直接写出![]() ,
,![]() 的数量关系;
的数量关系;
(3)若![]() 是美丽抛物线时,(2)
是美丽抛物线时,(2)![]() ,
,![]() 的数量关系成立吗?为什么?
的数量关系成立吗?为什么?
(4)系列美丽抛物线![]() (
(![]() 为小于
为小于![]() 的正整数)顶点在直线
的正整数)顶点在直线![]() 上,且它们中恰有两条美丽抛物线内接正方形面积比为
上,且它们中恰有两条美丽抛物线内接正方形面积比为![]() .求它们二次项系数之和.
.求它们二次项系数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
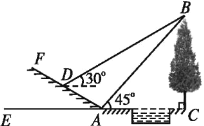
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )
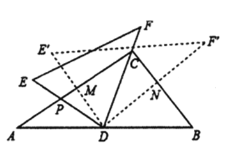
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
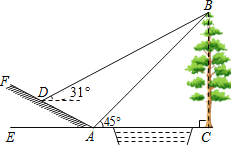
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com