
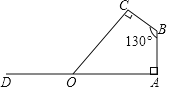
【题目】2018年底我市新湖一路贯通工程圆满竣工,若要在宽为40米的道路AD两边安装路灯,灯柱AB高10米,路灯的灯臂BC与灯柱AB成130°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路的中心线时照明效果最好,此时路灯的灯臂BC应为多少米?(结果精确到0.01)
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
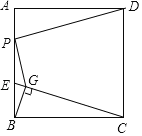
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是小明完成的一道作业题,请你参考小明的解答方法解答下面的问题:
小明的作业
计算:(-4)7×0.257
解:(-4)7×0.257=(-4×0.25)7
=(-1)7
=-1
(1)计算①82018×(-0.125)2018② ![]()
(2)看2·4n·16n=219 , 求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
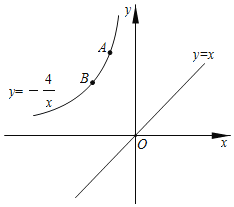
【题目】如图,反比例函数y=﹣![]() 在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1、﹣2,在直线y=x上求一点P,使PA+PB最小.则P点坐标为( )
在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1、﹣2,在直线y=x上求一点P,使PA+PB最小.则P点坐标为( )
A. P(![]() ,
,![]() )B. P(
)B. P(![]() ,
,![]() )C. P(1,1)D. P(
)C. P(1,1)D. P(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目:初中数学 来源: 题型:
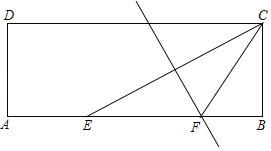
【题目】如图,在矩形ABCD中,AB=3BC,以点A为圆心,AD为半径画弧交AB于点E连接CE,作线段CE的中垂线交AB于点F,连接CF,则sin∠CFB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
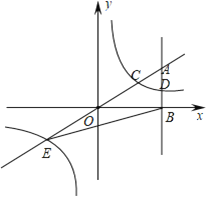
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,![]() =
=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式及点E的坐标;
(2)连接BC,求S△CEB.
(3)若在x轴上的有两点M(m,0)N(-m,0).
①以E、M、C、N为顶点的四边形能否为矩形?如果能求出m的值,如果不能说明理由.
②若将直线OA绕O点旋转,仍与y=![]() 交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com