
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
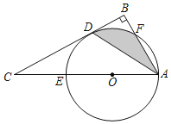
(1)求证:①BC是⊙O的切线;②CD2=CECA;
(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.
【答案】(1)①见解析,②见解析;(2)![]() .
.
【解析】
(1)①证明DO∥AB,即可求解;
②证明CDE∽△CAD,即可求解;
(2)证明△OFD、△OFA是等边三角形,S阴影=S扇形DFO,即可求解.
(1)①连接OD,
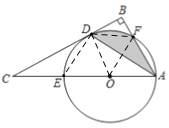
∵AD是∠BAC的平分线,
∴∠DAB=∠DAO,
∵OD=OA,
∴∠DAO=∠ODA,
∴∠DAO=∠ADO,
∴DO∥AB,而∠B=90°,
∴∠ODB=90°,
∴BC是⊙O的切线;
②连接DE,
∵BC是⊙O的切线,
∴∠CDE=∠DAC,
∠C=∠C,
∴△CDE∽△CAD,
∴![]() ,
,
∴CD2=CECA;
(2)连接DF、OF,
设圆的半径为r,
∵点F是劣弧AD的中点,
∴是OF是DA中垂线,
∴DF=AF,
∴∠FDA=∠FAD,
∵DO∥AB,
∴∠PDA=∠DAF,
∴∠ADO=∠DAO=∠FDA=∠FAD,
∴AF=DF=OA=OD,
∴△OFD、△OFA是等边三角形,
∴∠C=30°,
∴OD=![]() OC=(OE+EC),而OE=OD,
OC=(OE+EC),而OE=OD,
∴CE=OE=r=3,
S阴影=S扇形DFO=![]() ×π×32=
×π×32=![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
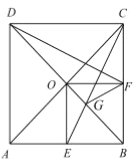
【题目】如图,在边长为1的正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到以下四个结论:①
,得到以下四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是________(填写序号).
,其中正确的结论是________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
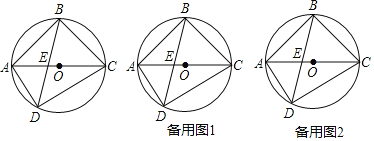
【题目】如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;
(3)在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点,
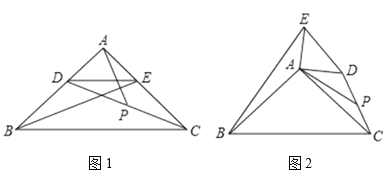
(1)(观察猜想)图1中,线段AP与BE的数量关系是 ,位置关系是 .
(2)(探究证明)把△ADE绕点A逆时针旋转到图2的位置,(1)中的猜想是否仍然成立?若成立请证明,否请说明理由;
(3)(拓展延伸)把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出线段AP长度的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
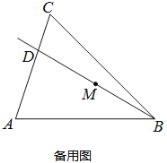
【题目】如图,在△ABC中,![]() ,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
(1)求线段BC的长;
(2)①当点D与点A、点C不重合时,过点D作DE⊥AB于点E,DF⊥BC于点F,连接ME,MF,在射线BD旋转的过程中,∠EMF的大小是否发生变化?若不变,求∠EMF的度数;若变化,请说明理由.
②在①的条件下,连接EF,直接写出△EFM面积的最小值______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备开展“阳光体育活动”,决定开设篮球、足球、乒乓球和羽毛球四种项目的活动,为了了解学生对这四项活动的喜欢情况,随机调查了该校a名学生最喜欢的一种项目(每名学生必选且只能选择这四项活动中的一种),并将调查结果绘制成如下的不完整的统计图:学生最喜欢的活动项目的人数条形统计图学生最喜欢的活动项目的人数扇形统计图
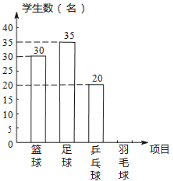
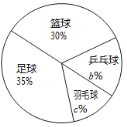
根据以上统计图提供的信息,解答下列问题:
(1)a=_____,b=______,c=______;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计该校1000名学生中有多少名学生最喜爱打篮球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
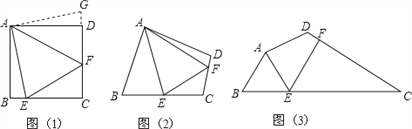
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
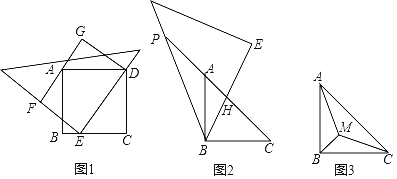
【题目】已知,把45°的直三角板的直角顶点E放在边长为6的正方形ABCD的一边BC上,直三角板的一条直角边经过点D,以DE为一边作矩形DEFG,且GF过点A,得到图1.
(1)求矩形DEFG的面积;
(2)若把正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC,把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC的直角顶点B重合,直三角板夹这个45°角的两边分别交CA和CA的延长线于点H、P,得到图2.猜想:CH、PA、HP之间的数量关系,并说明理由;
(3)若把边长为6的正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC,点M是Rt△ABC内一个动点,连接MA、MB、MC,设MA+MB+MC=y,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com