
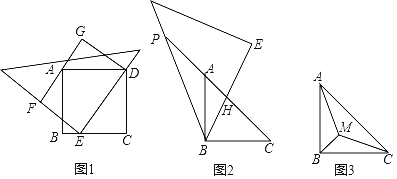
【题目】已知,把45°的直三角板的直角顶点E放在边长为6的正方形ABCD的一边BC上,直三角板的一条直角边经过点D,以DE为一边作矩形DEFG,且GF过点A,得到图1.
(1)求矩形DEFG的面积;
(2)若把正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC,把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC的直角顶点B重合,直三角板夹这个45°角的两边分别交CA和CA的延长线于点H、P,得到图2.猜想:CH、PA、HP之间的数量关系,并说明理由;
(3)若把边长为6的正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC,点M是Rt△ABC内一个动点,连接MA、MB、MC,设MA+MB+MC=y,直接写出![]() 的最小值.
的最小值.
【答案】(1)36;(2)CH2+PA2=HP2,理由见解析;(3)72+36![]() .
.
【解析】
(1)根据正方形的性质得到∠ADC=∠DCE=90°,根据矩形的性质得到∠AGD=∠GDE=90°,根据相似三角形的性质和矩形的面积公式即可得到结论;
(2)根据旋转的性质得到BK=BP,∠PBA=∠KBC,∠BCK=∠BAP=![]() =135°,由勾股定理得到
=135°,由勾股定理得到![]() ,求得∠PBA+∠ABE=45°,通过等量代换得到∠KBC+∠ABE=45°,根再据全等三角形的性质得到HK=HP,根据勾股定理即可得到结论;
,求得∠PBA+∠ABE=45°,通过等量代换得到∠KBC+∠ABE=45°,根再据全等三角形的性质得到HK=HP,根据勾股定理即可得到结论;
(3)根据旋转的性质得到MC=KN,BM=BK,根据等边三角形的性质得到MK=BM,于是得到MA+MB+MC=AM+MK+KN,当A,M,K,N四点共线时,AN就是所求的MA+MB+MC的最小值,过N作NQ⊥AB交AB的延长线于Q,求得AQ=AB+BQ=![]() ,再根据勾股定理即可得到结论.
,再根据勾股定理即可得到结论.
解:(1)∵四边形ABCD是正方形,
∴∠ADC=∠DCE=90°,
∵四边形DEFG是矩形,
∴∠AGD=∠GDE=90°,
∴∠DCE=∠AGD=90°,∠ADC=∠GDE=90°,
∴∠ADC﹣∠ADE=∠GDE﹣∠ADE,
∴∠EDC=∠ADG,
∵∠EDC=∠ADG,∠DCE=∠AGD=90°,
∴△ECD∽△AGD,
∴![]() ,
,
∴DGDE=DCDA=6×6=36,
∴矩形DEFG的面积=DGDE=36;
(2)![]() ,
,
证明:把△BAP绕着点B顺时针旋转90°得到△BCK,连接KH,
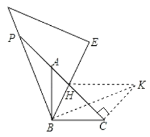
由旋转得△BAP≌△BCK,
∴BK=BP,∠PBA=∠KBC,∠BCK=∠BAP=![]() ,
,
∴∠HCK=![]() =
=![]() ,
,
∴由勾股定理得,![]() ,
,
∵∠PBE=45°,
∴∠PBA+∠ABE=45°,
∵∠PBA=∠KBC,
∴∠KBC+∠ABE=45°,
∵∠ABC=90°,
∴∠HBK=45°,
∵∠PBE=45°,
∴∠HBK=∠PBE=45°,
∵BK=BP,∠HBK=∠PBE,BH=BH,
∴△BHP≌△BHK(SAS
∴HK=HP,
∵![]() ,
,
∴![]() ;
;
(3)把△BMC绕着点B顺时针旋转60°得到△BKN,连接MK,BN,NC,
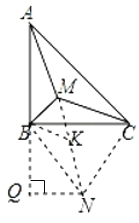
由旋转得,△BMC≌△BKN,
∴MC=KN,BM=BK,
∵BM=BK,∠MBK=60°,
∴△BKM是等边三角形,
∴MK=BM,
∴MA+MB+MC=AM+MK+KN,
当A,M,K,N四点共线时,AN就是所求的MA+MB+MC的最小值,
过N作NQ⊥AB交AB的延长线于Q,
∵![]() ,∠BQN=90°,
,∠BQN=90°,
∴QN=BNsin30°=6×![]() =3,BQ=BNcos30°=
=3,BQ=BNcos30°=![]() ,
,
∴AQ=AB+BQ=![]() ,
,
在Rt△AQN中,由勾股定理得, ![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
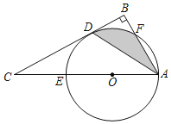
(1)求证:①BC是⊙O的切线;②CD2=CECA;
(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
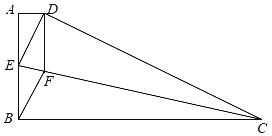
【题目】如图,四边形ABCD中,AD//BC,∠A=90°,CD=CB,过点C作∠DCB的平分线CE交AB于点E,连接DE,过点D作DF//AB,且交CE于F点,连接BF.
(1)求证:四边形DEBF是菱形;
(2)若AB=5,BC=13,求tan∠AED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
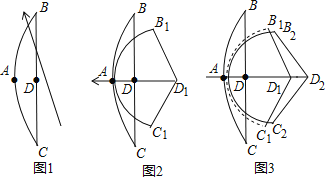
【题目】如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为______cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是 ,数轴上表示﹣2和3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点之间的距离表示为 ;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
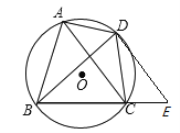
【题目】如图,四边形ABCD是⊙O的圆内接四边形,DE∥AC交BC的延长线于点E.
(1)求证:AB·DE=BD·DC;
(2)如果AD=CD,求证:DE为⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com