
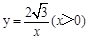 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.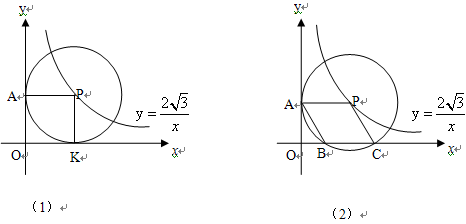
 ),B(1,0) C(3,0)
),B(1,0) C(3,0) .
.
 .sin60°=
.sin60°= ,即
,即
 ,PA=BC=2
,PA=BC=2 ),B(1,0) C(3,0).
),B(1,0) C(3,0). ),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=  ,利用sin∠PBG="PG/PB" ,列方程求x即可.
,利用sin∠PBG="PG/PB" ,列方程求x即可.

科目:初中数学 来源:不详 题型:解答题
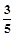 ,tan37°=
,tan37°=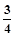 ,sin48°=
,sin48°=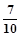 ,tan48°=
,tan48°=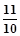 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
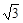 ≈1.732,结果保留整数).
≈1.732,结果保留整数).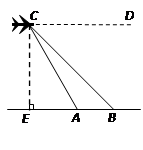
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com