
 Ј¬Ѕ«Т»їйЦ±ЅЗИэЅЗ°еµДЦ±ЅЗ¶ҐµгP·ЕЦГФЪ
Ј¬Ѕ«Т»їйЦ±ЅЗИэЅЗ°еµДЦ±ЅЗ¶ҐµгP·ЕЦГФЪ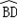 ЈЁІ»°ьАЁ¶ЛµгBЎўDЈ©ЙП»¬¶ЇЈ¬Т»МхЦ±ЅЗ±ЯНЁ№э¶ҐµгAЈ¬БнТ»МхЦ±ЅЗ±ЯУл±ЯBCПаЅ»УЪµгQЈ¬Б¬ЅУPCЈ¬ІўЙиPQ=xЈ¬ТФПВОТГЗ¶ФЎчCPQЅшРРСРѕїЈ®
ЈЁІ»°ьАЁ¶ЛµгBЎўDЈ©ЙП»¬¶ЇЈ¬Т»МхЦ±ЅЗ±ЯНЁ№э¶ҐµгAЈ¬БнТ»МхЦ±ЅЗ±ЯУл±ЯBCПаЅ»УЪµгQЈ¬Б¬ЅУPCЈ¬ІўЙиPQ=xЈ¬ТФПВОТГЗ¶ФЎчCPQЅшРРСРѕїЈ®
 Ј¬
Ј¬ Ј¬
Ј¬ Ј¬
Ј¬ ©Ѓ1Ј¬
©Ѓ1Ј¬ ©Ѓ1=
©Ѓ1=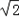 Ј¬
Ј¬ Ј®
Ј®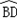 УЪP0Ј¬ФтP0Q=BQ=xЈ¬ЎПP0CQ=45ЎгЈ¬ЎПCP0Q=90ЎгЈ»
УЪP0Ј¬ФтP0Q=BQ=xЈ¬ЎПP0CQ=45ЎгЈ¬ЎПCP0Q=90ЎгЈ»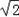 ©Ѓ1Ј¬ЎПPQC=ЎПPABЈј90ЎгЈ¬ЎПPCQЈј90ЎгЈ®
©Ѓ1Ј¬ЎПPQC=ЎПPABЈј90ЎгЈ¬ЎПPCQЈј90ЎгЈ®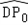 ЙПФЛ¶ЇК±Ј¬
ЙПФЛ¶ЇК±Ј¬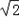 ©Ѓ1Ј®
©Ѓ1Ј®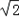 ©Ѓ1Ј®
©Ѓ1Ј®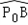 ЙПФЛ¶ЇК±Ј¬
ЙПФЛ¶ЇК±Ј¬ ©Ѓ1.
©Ѓ1.


 ХгґуУЕѧСѧДкј¶ПОЅУЅЭѕ¶ХгЅґуС§іц°жЙзПµБРґр°ё
ХгґуУЕѧСѧДкј¶ПОЅУЅЭѕ¶ХгЅґуС§іц°жЙзПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
| ¦Р | 2 |

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ИзНјЈ¬±Яі¤ОЄ6µДХэ·ЅOABCµД¶ҐµгOФЪЧш±кԵ㴦Ј¬µгAЎўC·Ц±рФЪxЦбЎўyЦбµДХэ°лЦбЙПЈ¬µгEКЗOA±ЯЙПµДµгЈЁІ»УлµгAЦШєПЈ©Ј¬EFЎНCEЈ¬ЗТУлХэ·ЅРОНвЅЗЖЅ·ЦПЯACЅ»УЪµгPЈ®
ИзНјЈ¬±Яі¤ОЄ6µДХэ·ЅOABCµД¶ҐµгOФЪЧш±кԵ㴦Ј¬µгAЎўC·Ц±рФЪxЦбЎўyЦбµДХэ°лЦбЙПЈ¬µгEКЗOA±ЯЙПµДµгЈЁІ»УлµгAЦШєПЈ©Ј¬EFЎНCEЈ¬ЗТУлХэ·ЅРОНвЅЗЖЅ·ЦПЯACЅ»УЪµгPЈ®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
 ИзНјЈ¬±Яі¤ОЄ6µДХэ·ЅOABCµД¶ҐµгOФЪЧш±кԵ㴦Ј¬µгAЎўC·Ц±рФЪxЦбЎўyЦбµДХэ°лЦбЙПЈ¬µгEКЗOA±ЯЙПµДµгЈЁІ»УлµгAЦШєПЈ©Ј¬EFЎНCEЈ¬ЗТУлХэ·ЅРОНвЅЗЖЅ·ЦПЯACЅ»УЪµгPЈ®
ИзНјЈ¬±Яі¤ОЄ6µДХэ·ЅOABCµД¶ҐµгOФЪЧш±кԵ㴦Ј¬µгAЎўC·Ц±рФЪxЦбЎўyЦбµДХэ°лЦбЙПЈ¬µгEКЗOA±ЯЙПµДµгЈЁІ»УлµгAЦШєПЈ©Ј¬EFЎНCEЈ¬ЗТУлХэ·ЅРОНвЅЗЖЅ·ЦПЯACЅ»УЪµгPЈ®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
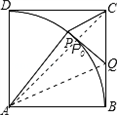
ИзНјЅ«±Яі¤ОЄ1µДХэ·ЅРОOAPBСШ![]() ЦбХэ·ЅПтБ¬Рш·ЧЄ2006ґОЈ¬µгPТАґОВдФЪµг
ЦбХэ·ЅПтБ¬Рш·ЧЄ2006ґОЈ¬µгPТАґОВдФЪµг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎЎ
Ј¬ЎЎ![]() µДО»ЦГЈ¬Фт
µДО»ЦГЈ¬Фт![]() µДєбЧш±к
µДєбЧш±к![]() ЈЅ_________Ј®
ЈЅ_________Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє2012-2013С§ДкРВИЛЅМ°жѕЕДкј¶ЈЁЙПЈ©ЖЪЦРКэС§КФѕнЈЁ7Ј©ЈЁЅвОц°жЈ© МвРНЈєЅвґрМв

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com