Question

如图所示，已知△ABC为等腰直角三角形，且EC⊥AC于C，AE=BF，试判断AE和BF的位置关系并说明理由．

Answer 1

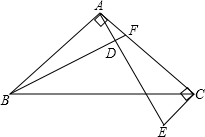
解：AE⊥BF．
理由如下：∵△ABC为等腰直角三角形，
∴AB=AC，
又EC⊥AC于C，
∴在Rt△ABF与Rt△CAE中，
，
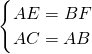
∴△ABF≌△CAE（HL），
∴∠ABF=∠EAC，
∵∠EAC+∠BAD=90°，
∴∠ABF+∠BAD=90°，
∴∠ADB=180°-（∠ABF+∠BAD）=180°-90°=90°．
∴AE⊥BF．
分析：先利用HL定理证明△ABF与△CAE全等，根据全等三角形对应角相等可以得到∠ABF=∠EAC，然后利用角度的转换即可得到∠ADB=90°，从而判断出AE和BF的位置关系是垂直．
点评：本题考查了全等三角形的判定与性质，等腰直角三角形的性质，证明直角三角形全等除一般的三角形的全等判定方法外，还有特殊的“HL”判定方法．
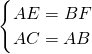