
【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,求证EG=FG.(提示:先证△ABF≌△CDE,得BF=DE,再证△BFG≌△DEG);若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
【1】求证:△ABE≌△CDA;
【2】若∠DAC=40°,求∠EAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段话,并解决后面的问题 .观察下面一例数:
1,2,4,8,……
我们发现,这一列数从第2项起,每一项与它前一项的比都等于2 .
一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比 .
(1)等比数列5,-15,45,……的第4项是 ;
(2)如果一列数![]() ,
,![]() ,
,![]() ,
,![]() ,……是等比数列,且公比为q,那么根据上述的规定,有
,……是等比数列,且公比为q,那么根据上述的规定,有
![]() ,
,![]() ,
,![]() ,……
,……
所以![]() ,
,
![]() ,
,
![]() ,
,
……
![]() .(用
.(用![]() 与q的代数式表示)
与q的代数式表示)
(3)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在四边形ABCD中,∠A=90°.若AB=4cm,AD=3cm,CD=12cm,BC=13cm,
(1)请说明BD⊥CD;
(2)求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家住房结构如图所示,图中标了有关尺寸(墙体厚度忽略不计,单位:米)房屋的主人计划把卧室以外的地面都铺上地砖.
(1)如果他选用地砖的价格是 a 元/平方米,则买地砖至少需用多少元(图中标了有关尺寸(墙体厚度忽略不计,单位:米)
(2)如果房屋的高度为 h 米,现需要在客厅和卧室的墙上贴壁纸,至少需要多少平方米的壁纸?(计算时不扣除门、窗所占的面积,结果用代数式表示)?

查看答案和解析>>
科目:初中数学 来源: 题型:
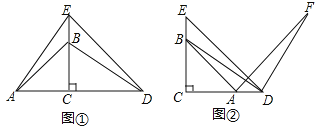
【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是正方形
是正方形![]() 内一点,以点
内一点,以点![]() 为旋转中心,将
为旋转中心,将![]() 按顺时针方向旋转使点
按顺时针方向旋转使点![]() 与点
与点![]() 重合,这时
重合,这时![]() 点旋转到
点旋转到![]() 点.
点.

![]() 设
设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,在图中用阴影标出
,在图中用阴影标出![]() 旋转到
旋转到![]() 的过程中,边
的过程中,边![]() 所扫过区域的面积,并用含
所扫过区域的面积,并用含![]() 、
、![]() 的式子表示它________;
的式子表示它________;
![]() 若
若![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,试猜想
,试猜想![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则![]() 的值等于_____.
的值等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com