
如图,已知正方形ABCD,点E是BC上一点,
以AE为边作正方形AEFG。
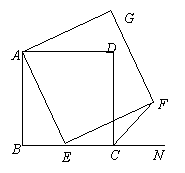 (1)连结GD,求证△ADG≌△ABE;
(1)连结GD,求证△ADG≌△ABE;
(2)连结FC,求证∠FCN=45°;
(3)请问在AB边上是否存在一点Q,
使得四边形DQEF是平行四边形?
若存在,请证明;若不存在,请说明理由。
1)如图,连接DG
∵四边形ABCD和四边形AEFG是正方形
∴DA=BA,EA=GA,∠BAD=∠EAG=90°
∴∠DAG=∠BAE
∴△ADG≌△ABE;
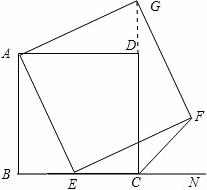 (2)过F作BN的垂线,设垂足为H
(2)过F作BN的垂线,设垂足为H
∵∠BAE+∠AEB=90°,∠FEH+∠AEB=90°
∴∠BAE=∠HEF
∵AE=EF
∴△ABE≌△EHF
∴AB=EH,BE=FH
∴AB=BC=EH
∴BE+EC=EC+CH
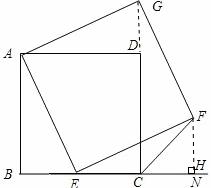 ∴CH=BE=FH
∴CH=BE=FH
∴∠FCN=45°;
(3)在AB上取AQ=BE,连接QD
∵AB=AD
∴△DAQ≌△ABE
∵△ABE≌△EHF
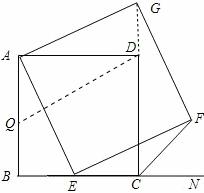 ∴△DAQ≌△ABE≌△ADG
∴△DAQ≌△ABE≌△ADG
∴∠GAD=∠ADQ
∴AG、QD平行且相等
又∵AG、EF平行且相等
∴QD、EF平行且相等
∴四边形DQEF是平行四边形
∴在AB边上存在一点Q,使得四边形DQEF
是平行四边形.


科目:初中数学 来源: 题型:
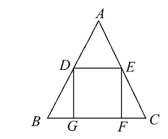
如图,△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
A.3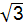 cm B.4cm
cm B.4cm
C.2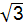 cm D.2
cm D.2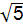 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
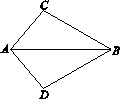
如图,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,
∠ADB=100°,则∠BAC的度数是( ).
A.30° B.100° C.50° D.80°
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形 的边长为4,将一个足够大的直角三角板的直角顶点放于点
的边长为4,将一个足够大的直角三角板的直角顶点放于点 处,该三角板的两条直角边与
处,该三角板的两条直角边与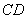 交于点
交于点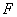 ,与
,与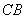 延长线交于点
延长线交于点 .四边形
.四边形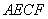 的面积是( )A. 16 B.12 C.8 D.4
的面积是( )A. 16 B.12 C.8 D.4

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com