
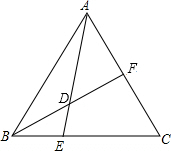
 如图,在△ABC中,E是BC上一点,EC=2BE,点F是AC的中点,若S△ABC=12,求S△ADF-S△BED的值.
如图,在△ABC中,E是BC上一点,EC=2BE,点F是AC的中点,若S△ABC=12,求S△ADF-S△BED的值. 分析 利用三角形面积公式,等高的三角形的面积比等于底边的比,则S△AEC=$\frac{2}{3}$S△ABC=8,S△BCF=$\frac{1}{2}$S△ABC=6,然后利用S△ADF-S△BED=S△AEC-S△BCF=2即可得到答案.
解答 解:∵EC=2BE,
∴S△AEC=$\frac{2}{3}$S△ABC=$\frac{2}{3}$×12=8,
∵点F是AC的中点,
∴S△BCF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12=6,
∴S△AEC-S△BCF=2,
即S△ADF+S四边形CEDF-(S△BDE+S四边形CEDF)=2,
∴S△ADF-S△BED=2.
点评 本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即S△=$\frac{1}{2}$×底×高;三角形的中线将三角形分成面积相等的两部分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
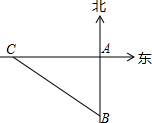 如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 变成原来的10倍 | B. | 缩小为原来的10倍 | ||
| C. | 是原来的$\frac{2}{3}$ | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
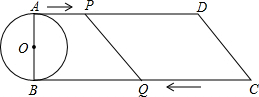 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动.P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t s,问:
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动.P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t s,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com