
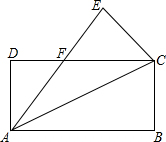
 根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形
根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形分析 由折叠的性质得出∠BAC=∠FAC,由平行四边形的性质得出∠BAC=∠FCA,得出∠FAC=∠FCA,证出FA=FC即可.
解答 已知:如图,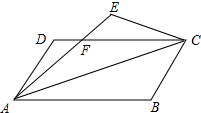 将平行四边形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F;
将平行四边形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F;
求证:折叠后的重叠部分(即△FAC)是等腰三角形;
证明:∵将平行四边形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,
∴∠BAC=∠FAC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAC=∠FCA,
∴∠FAC=∠FCA,
∴FA=FC,
即△FAC是等腰三角形.
点评 本题考查了平行四边形的性质、翻折变换的性质、等腰三角形的判定;熟练掌握翻折变换和平行四边形的性质,弄清角之间的相等关系是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
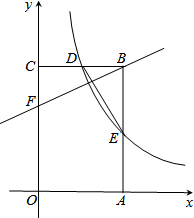 如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0),的图象经过BC上的点D与AB交于点E,连接DE,若若E是AB的中点﹒
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0),的图象经过BC上的点D与AB交于点E,连接DE,若若E是AB的中点﹒查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的方程x2+(m-2)x+m-3=0.
已知关于x的方程x2+(m-2)x+m-3=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
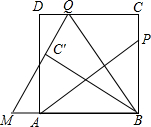 如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com