解:(1)∵点E(2,0)绕点O顺时针旋转90°后对应点是点C,
∴C(0,-2);
代入抛物线的解析式中,得:
2a=-2,
即a=-1;
∴该抛物线的解析式为:y=x
2-x-2.
(2)易知:A(-1,0),B(2,0),C(0,-2);
则AB=3,OC=2.
∵四边形A
1B
1C
1F是矩形,则FC
1∥AB,
∴△CC
1F∽△CBA,
得:

,
故FC
1=

(2-a);
∴S=A
1F•FC
1=a×

(2-a)=-

(a
2-2a);
即:S=-

(a-1)
2+

,
即当a=1时,S
最大=

.
(3)假设存在符合条件的M、N点,则:
①以OP为平行四边形的边长;
设M(a,a
2-a-2),则N(a-4,a
2-a-4);
由于N点在抛物线的图象上,
(a-4)
2-(a-4)-2=a
2-a-4,
解得a=

,
故M(

,
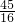
),N(-

,

);
②以OP为平行四边形对角线:先求出OP中点坐标为(2,1),
设M(a,a
2-a-2),则N(4-a,-a
2+a+4);
将N点坐标代入抛物线解析式,
得:(4-a)
2-(4-a)-2=-a
2+a+4,
解得a=3或1,
则M,N的坐标分别为(3,4),(1,-2)或(1,-2),(3,4);
因此存在符合条件的M、N点,它们的坐标为:
M(

,
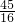
),N(-

,

)或M(-

,

),N(

,
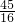
)或M(3,4),N(1,-2)或M(1,-2),N(3,4).
分析:(1)由于点E(2,0)绕点O顺时针旋转90°后得到点C,那么C(0,-2),将它的坐标代入抛物线的解析式中,即可求出a的值,从而确定该抛物线的解析式.
(2)根据(1)所得抛物线的解析式,即可求出A、B的坐标,在△ABC中,易求得AB、OC的长,而△CC
1F∽△CBA,根据得到的比例线段,即可求得FC
1的表达式,从而根据矩形的面积公式求出S、a的函数关系式.
(3)此题应分作两种情况考虑:
①以OP为平行四边形的边,那么MN平行且相等于OP,可设出点M的坐标,根据O、P的坐标可知M、N的横坐标的差为4,纵坐标的差为2,可据此表示出点N的坐标,然后代入抛物线的解析式中,即可求得M、N的坐标;
②以OP为平行四边形的对角线,首先求出OP中点(即平行四边形对角线的交点)的坐标,设出点M坐标后,仿照①的方法表示出点N的坐标,再代入抛物线的解析式中求得M、N的坐标即可.
点评:此题考查了图形的旋转变换、二次函数解析式的确定、图形面积的求法以及平行四边形的判定等重要知识点,在(3)题中,由于OP是平行四边形的边还是对角线并不确定,因此一定要分类讨论,以免漏解.


 ,
, (2-a);
(2-a); (2-a)=-
(2-a)=- (a2-2a);
(a2-2a); (a-1)2+
(a-1)2+ ,
, .
. ,
, ,
,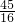 ),N(-
),N(- ,
, );
); ,
,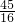 ),N(-
),N(- ,
, )或M(-
)或M(- ,
, ),N(
),N( ,
,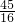 )或M(3,4),N(1,-2)或M(1,-2),N(3,4).
)或M(3,4),N(1,-2)或M(1,-2),N(3,4).

 在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案.
在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案. 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,