
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小;
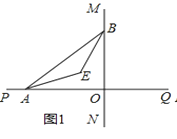
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;

(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,在△AEF中,如果有一个角是另一个角的4倍,试求∠ABO的度数.
【答案】(1)∠AEB的大小不变(2)∠CED的大小不变(3)∠ABO为45°或36°
【解析】分析:(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=![]() ∠OAB,∠ABE=
∠OAB,∠ABE=![]() ∠ABO,由三角形内角和定理即可得出结论;(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出∠OAB+∠OBA=90°,故∠PAB+∠MBA=270°,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知∠BAD=
∠ABO,由三角形内角和定理即可得出结论;(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出∠OAB+∠OBA=90°,故∠PAB+∠MBA=270°,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知∠BAD=![]() ∠BAP,∠ABC=
∠BAP,∠ABC=![]() ∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;(3))由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=
∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;(3))由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=![]() ∠BAO,∠EOQ=
∠BAO,∠EOQ=![]() ∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的4倍分四种情况进行分类讨论.
∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的4倍分四种情况进行分类讨论.
本题解析:
(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=![]() ∠OAB,∠ABE=
∠OAB,∠ABE=![]() ∠ABO,
∠ABO,
∴∠BAE+∠ABE=![]() (∠OAB+∠ABO)=45°,∴∠AEB=135°;
(∠OAB+∠ABO)=45°,∴∠AEB=135°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=![]() ∠BAP,∠ABC=
∠BAP,∠ABC=![]() ∠ABM,
∠ABM,
∴∠BAD+∠ABC=![]() (∠PAB+∠ABM)=135°,
(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°; (其它方法酌情给分)
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=![]() ∠BAO,∠EOQ=
∠BAO,∠EOQ=![]() ∠BOQ,
∠BOQ,
∴∠E=∠EOQ-∠EAO=(∠BOQ-∠BAO)=![]() ∠ABO,
∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,∵有一个角是另一个角的4倍,故有:
①∠EAF=4∠E,∠E=22.5°,∠ABO=45°;
②∠EAF=4∠F,∠E=67.5°,∠ABO=135°(不合题意,舍去);
③∠F=4∠E,∠E=18°,∠ABO=36°;
④∠E=3∠F,∠E=72°,∠ABO=144°(不合题意,舍去).
∴∠ABO为45°或36°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
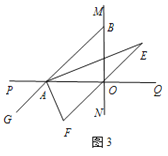
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,∠DCB=30°.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
(4)若将图2中△ABC绕顶点B按顺时针方向旋转a度(0°<a<90°),得到△DBE,连接AD、DC,则∠DCB= °,四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题①同旁内角互补,两直线平行;②全等三角形的周长相等;③直角都相等;④等边对等角。它们的逆命题是真命题的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
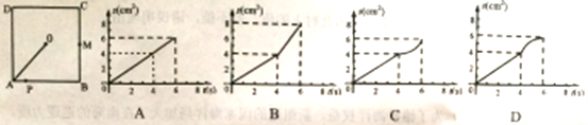
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图像可以是( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+bx﹣1.
(1)求证:无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)若两点P(﹣3,m)和Q(1,m)在该函数图象上.
①求b、m的值;
②将二次函数图象向上平移多少单位长度后,得到的函数图象与x轴只有一个公共点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com