
【题目】.如图,反比例函数y=k/x图像与直线y=-x交于A,B两点, 将双曲线右半支沿射线AB方向平移与左半支交于C,D. 点A到达A’点, A’B=BO, CE=6![]() . 则k=______.
. 则k=______.
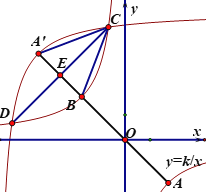
【答案】-![]()
【解析】
先解方程组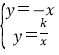 得B(-
得B(-![]() ,
,![]() ),再利用B点为OA′的中点得到A′(-2
),再利用B点为OA′的中点得到A′(-2![]() ,2
,2![]() ),利用反比例函数图象的对称性得到C、D关于直线AB对称,则E点为A′B的中点,所以E(-
),利用反比例函数图象的对称性得到C、D关于直线AB对称,则E点为A′B的中点,所以E(-![]() ,
,![]() ),作CH∥y轴,EH∥x轴,如图,证明△CEH为等腰直角三角形得到EH=CH=
),作CH∥y轴,EH∥x轴,如图,证明△CEH为等腰直角三角形得到EH=CH=![]() CE=6,则C点坐标为(6-
CE=6,则C点坐标为(6-![]() ,6+
,6+![]() ),然后把C(6-
),然后把C(6-![]() ,6+
,6+![]() )代入y=
)代入y=![]() 得(6-
得(6-![]() )(6+
)(6+![]() )=k,最后解方程求出k即可.
)=k,最后解方程求出k即可.
解:解方程组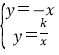 得
得![]() 或
或![]() ,则B(-
,则B(-![]() ,
,![]() ),
),
∵A′B=BO,
∴B点为OA′的中点,
∴A′(-2![]() ,2
,2![]() ),
),
∵双曲线右半支沿射线AB方向平移与左半支交于C,D.
∴C、D关于直线AB对称,
∴E点为A′B的中点,
∴E(-![]() ,
,![]() ),
),
作CH∥y轴,EH∥x轴,如图,
∴CD⊥AB,
∴CD与x轴所夹的锐角为45°,
∴△CEH为等腰直角三角形,
∴EH=CH==![]() CE=
CE=![]() ×6
×6![]() =6,
=6,
∴C点坐标为(6-![]() ,6+
,6+![]() ),
),
把C点坐标代入y=![]() 得(6-
得(6-![]() )(6+
)(6+![]() )=k,
)=k,
解得k=-![]()
故答案为:-![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加,据统计,某小区![]() 年底拥有家庭轿车
年底拥有家庭轿车![]() 辆,
辆,![]() 年底家庭轿车的拥有量达到
年底家庭轿车的拥有量达到![]() 辆.
辆.
(1)若该小区![]() 年底到
年底到![]() 年底家庭轿车拥有量的年平均增长率都相同,求该小区到
年底家庭轿车拥有量的年平均增长率都相同,求该小区到![]() 年底家庭轿车将达到多少辆?
年底家庭轿车将达到多少辆?
(2)为了解决停车困难,该小区决定投资![]() 万元再建造若干个停车位,据测算,室内车位建造费用
万元再建造若干个停车位,据测算,室内车位建造费用![]() 元
元![]() 个,露天车位建造费用
个,露天车位建造费用![]() 元
元![]() 个,考虑到实际因素,计划露天车位的数量不少于室内车位的
个,考虑到实际因素,计划露天车位的数量不少于室内车位的![]() 倍,但不超过室内车位的
倍,但不超过室内车位的![]() 倍,求该小区建造车位共有几种方案?
倍,求该小区建造车位共有几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从A地出发,沿同一条笔直的公路匀速前往相距360km的B地,半小时后甲发现有东西落在A地,于是立即以原速返回A地取物品,取到物品后立即以比原来速度每小时快15km继续前往B地(所有掉头时问和领取物品的时问忽略不计),甲、乙两车之间的距离y(km)与甲车行驶的时间x(h)之问的部分函数关系如图所示:当甲车到达B地时,乙车离B地的距离是多少.
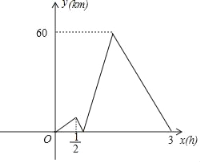
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F, (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r=![]() (a+b-c).
(a+b-c).
(2) 若AD交圆于P, PC交圆于H, FH//BC, 求∠CPD;
(3)若r=3![]() , PD=18, PC=27
, PD=18, PC=27![]() . 求△ABC各边长.
. 求△ABC各边长.
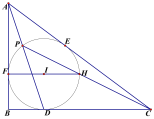
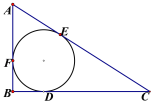
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是 .
A.小明打开的一定是楼梯灯
B.小明打开的可能是卧室灯
C.小明打开的不可能是客厅灯
D.小明打开走廊灯的概率是![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为10的半圆形量角器中,而一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是
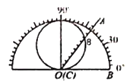
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:
已知:如图,直线 l 和直线 l 外一点 A
求作:直线 AP,使得 AP∥l
作法:如图
① 在直线 l 上任取一点 B,以点 A 为圆心,AB 为半径作圆,与直线 l 交于 B,C 两点.
② 连接 AC,AB,延长 BA 交⊙A 于点 D;
③ 作∠DAC 的平分线 AP,并反向延长.
所以直线 AP 就是所求作的直线
根据小星同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明
证明:∵AB=AC,
∴∠ABC=∠ACB( ① )(填推理的依据)
∵∠DAC 是△ABC 的外角,
∴∠DAC=∠ABC+∠ACB
∴∠DAC=2∠ABC
∵AP 平分∠DAC,
∴∠DAC=2∠DAP
∴ ②
∴AP∥l( ③ )(填推理的依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com