
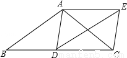
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据平行四边形的性质、等腰三角形的性质,利用全等三角形的判定定理SAS可以证得△ADC≌△ECD;
(2)利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(对边平行且相等是四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
试题解析:证明:(1)∵四边形ABDE是平行四边形
∴AB∥DE,AB=DE;
∴∠B=∠EDC;
又∵AB=AC,
∴AC=DE,
∠B=∠ACB,
∴∠EDC=∠ACD
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形
∴BD∥AE,BD=AE
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换)
∴四边形ADCE是平行四边形;
在△ABC中,
AB=AC,
BD=CD,
∴AD⊥BC,
∴∠ADC=90°,
∴?ADCE是矩形.
考点: 1.矩形的判定;2.全等三角形的判定与性质;3.等腰三角形的性质;4.平行四边形的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:解答题
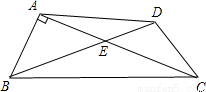
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=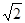 ,BE=2
,BE=2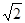 .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一次函数、反比例函数与几何图形结合(解析版) 题型:解答题
如图,一次函数y=kx+1(k≠0)与反比例函数y= 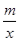 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
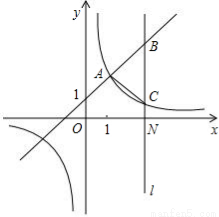
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:选择题
已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
A.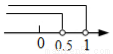
B.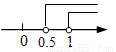
C.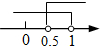
D.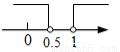
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:解答题
已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:填空题
某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为_____.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:解答题
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.
求证:AC∥DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com