
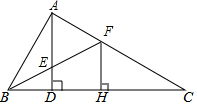
 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线BF交AD于点E,交AC于点F,FH⊥BC于点H,求证:AE=FH.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线BF交AD于点E,交AC于点F,FH⊥BC于点H,求证:AE=FH. 分析 根据角平分线上的点到两边的距离相等可得:FH=FA;则只要在确定FA与AE的关系即可确定AE与FH之间的关系;在直角三角形AFB中∠AFB+∠ABF=90°,在直角三角形BDE中,∠DEB+∠EBD=90°,根据角平分线的性质可知:∠ABF=∠DBE,则∠AFB=∠DEB,又知∠AEF=∠DEB,则∠AFB=∠AEF,所以AE=FA,则AE=FH.
解答 证明:∵BF平分∠ABC,FA⊥AB,FH⊥BC,
∴FH=FA,
∵∠AFB+∠ABF=90°,∠DEB+∠EBD=90°,且∠ABF=∠EBD,
∴∠AFB=∠DEB,
∵∠AEF=∠DECB,
∴∠AFB=∠AEF,
∴AE=FA,
∴AE=FH.
点评 本题主要考查了等腰三角形的判定和性质,角平分线的性质;解题时利用了AF这个中间量进行了等量代换是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
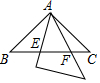 如图,两个全等的等腰直角三角板(斜边长为2)如图放置,其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合.若三角板ABC固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边BC交于点E、F.设BF=x,CE=y,则y关于x的函数图象大致是( )
如图,两个全等的等腰直角三角板(斜边长为2)如图放置,其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合.若三角板ABC固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边BC交于点E、F.设BF=x,CE=y,则y关于x的函数图象大致是( )| A. | 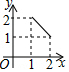 | B. | 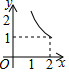 | C. | 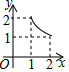 | D. | 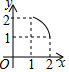 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
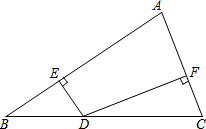 如图,在△ABC中,AB=20cm,AC=12cm,点D在BC边上,作DE⊥AB于E、DF⊥AC于F,若DE=5cm,△ABC的面积为122cm2,则DF的长为( )
如图,在△ABC中,AB=20cm,AC=12cm,点D在BC边上,作DE⊥AB于E、DF⊥AC于F,若DE=5cm,△ABC的面积为122cm2,则DF的长为( )| A. | 9 cm | B. | 10 cm | C. | 11 cm | D. | 12 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,2016年9月25日,有着中国“天眼”之称的500米口径球面射电望远镜(FAST)在贵州省平塘县落成启用,它将在未来10年到20年保持国际一流设备的地位.其反射面积约2.5×105平方米,相当于( )个面积为5×103平方米的足球场.
如图,2016年9月25日,有着中国“天眼”之称的500米口径球面射电望远镜(FAST)在贵州省平塘县落成启用,它将在未来10年到20年保持国际一流设备的地位.其反射面积约2.5×105平方米,相当于( )个面积为5×103平方米的足球场.| A. | 5 | B. | 50 | C. | 500 | D. | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )
如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com