
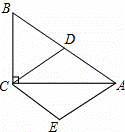
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
科目:初中数学 来源: 题型:
小明开了一家网店,进行社会实践,计划经销甲、乙两种商品.若甲商品每件利润10元,乙商品每件利润20元,则每周能卖出甲商品40件,乙商品20件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可各多销售10件.为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.
(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式:y甲= 10x+40 ,y乙= 10x+20 ;
(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式?如果每周甲商品的销售量不低于乙商品的销售量的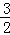 ,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
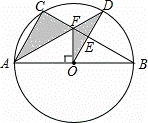
.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2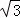 .
.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:空气质量指数统计表
级别 指数 天数 百分比
优 0﹣50 24 m
良 51﹣100 a 40%
轻度污染 101﹣150 18 15%
中度污染 151﹣200 15 12.5%
重度污染 201﹣300 9 7.5%
严重污染 大于300 6 5%
合计 120 100%
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a= ,m= ;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是 度;
(4)估计该市2014年(365天)中空气质量指数大于100的天数约有 天.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com