
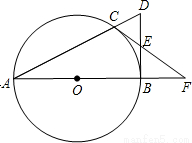
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.
(1)求证:CF是⊙O的切线;
(2)若ED=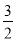 ,tanF=
,tanF=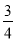 ,求⊙O的半径.
,求⊙O的半径.
(1)证明见解析;(2)3.
【解析】
试题分析:(1)连CB、OC,根据切线的性质得∠ABD=90°,根据圆周角定理由AB是直径得到∠ACB=90°,即∠BCD=90°,则根据直角三角形斜边上的中线性质得CE=BE,所以∠BCE=∠CBE,所以∴OBC+∠CBE=∠OCB+∠BCE=90°,然后根据切线的判定定理得CF是⊙O的切线.
(2)CE=BE=DE=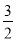 ,在Rt△BFE中,利用正切的定义得
,在Rt△BFE中,利用正切的定义得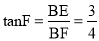 ,可计算出BF=2,再利用勾股定理可计算出EF=
,可计算出BF=2,再利用勾股定理可计算出EF=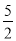 ,所以CF=CE+EF=4,然后在Rt△OCF中,利用正切定义可计算出OC.
,所以CF=CE+EF=4,然后在Rt△OCF中,利用正切定义可计算出OC.
试题解析:(1)如图,连接CB、OC,
∵BD为⊙O的切线,∴DB⊥AB。∴∠ABD=90°.
∵AB是直径,∴∠ACB=90°.
∴∠BCD=90°.
∵E为BD的中点,∴CE=BE. ∴∠BCE=∠CBE.
而∠OCB=∠OBC,
∴∠OBC+∠CBE=∠OCB+∠BCE=90°.
∴OC⊥CF,
∴CF是⊙O的切线;
(2)【解析】
CE=BE=DE=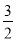 ,
,
在Rt△BFE中,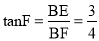 ,∴BF=2.
,∴BF=2.
∴ .∴CF=CE+EF=4.
.∴CF=CE+EF=4.
在Rt△OCF中,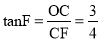 ,∴OC=3,即⊙O的半径为3.
,∴OC=3,即⊙O的半径为3.
考点:1.切线的判定和性质;2.勾股定理;3.圆周角定理;4.等腰三角形的性质.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源:2014年初中毕业升学考试(内蒙古包头、乌兰察布卷)数学(解析版) 题型:填空题
如图,AB是⊙O的直径,BC是弦,点E是 的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 .
的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:解答题
列方程(组)解应用题:
某市计划建造80万套保障性住房,用于改善百姓的住房状况.开工后每年建造保障性住房的套数比原计划增加25%,结果提前两年保质保量地完成了任务.求原计划每年建造保障性住房多少万套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com