
【题目】如图甲是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图乙围成一个较大的正方形.

(1)请用两种方法表示图中阴影部分面积(只需表示,不必化简);
(2)比较(1)两种结果,你能得到怎样的等量关系?
请你用(2)中得到等量关系解决下面问题:如果m﹣n=5,mn=14,求m+n的值.
【答案】(1)(m+n)2﹣4mn;(m﹣n)2;
(2)m+n的值为9.
【解析】
试题分析:(1)观察图形可确定:方法一,大正方形的面积为(m+n)2,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)2﹣4mn;
方法二,图2中阴影部分为正方形,其边长为m﹣n,所以其面积为(m﹣n)2.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)2﹣4mn=(m﹣n)2.由(2)得,将m﹣n=5,mn=14,代入(2)式可求m+n=9.
解:(1)方法一:∵大正方形的面积为(m+n)2,四个小长方形的面积和为4mn,
∴中间阴影部分的面积为(m+n)2﹣4mn.
方法二:∵中间小正方形的边长为m﹣n,∴其面积为(m﹣n)2.
(2)(m+n)2﹣4mn=(m﹣n)2.
∵m﹣n=5,mn=14,
∴(m+n)2﹣4×14=52,得m+n=9或m+n=﹣9(舍),
故m+n的值为9.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.
(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积; (3)、点P是第一象限角平分线上一点,若![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用普查方式的是( )
A.调查一批汽车的使用寿命
B.调查重庆全市市民“五一”期间计划外出旅游
C.调查某航班的旅客是否携带了违禁物品
D.调查全国初三学生的视力情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间甲、乙两家商店都打出了促销优惠招牌,已知这两家商店以相同的价格出售同样的商品,两家商店的优惠方案如下:在甲商店累计购买商品超过500元后,超过部分按原价七折优惠;在乙商店购买商品只按原价的八折优惠;设顾客累计购物![]() 元(
元(![]() )
)
(1)用含![]() 的整式分别表示顾客在两家商店购买所付的费用.
的整式分别表示顾客在两家商店购买所付的费用.
(2)当![]() 时,试比较顾客到哪家商店购物更加优惠.
时,试比较顾客到哪家商店购物更加优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月20日,2016长安汽车重庆国际马拉松鸣枪开跑,本届重马不仅是2016年全国马拉松锦标赛三站中的一站,同时还是2016年巴西里约奥运会马拉松唯一一站选拔赛,比赛分为全程、半程、迷你三大项目,吸引了31900多名选手参加.把数“31900”用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣![]() x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
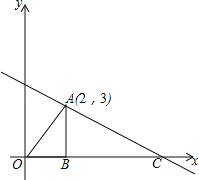
(1)求此一次函数的解析式,并求出一次函数与x轴的交点C的坐标;
(2)设点P为直线y=﹣![]() x+b在第一象限内的图象上的一动点,求△OBP的面积S与x之间的函数关系式,并写出自变量x的范围;
x+b在第一象限内的图象上的一动点,求△OBP的面积S与x之间的函数关系式,并写出自变量x的范围;
(3)设点M为坐标轴上一点,且S△MAC=24,直接写出所有满足条件的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com