Question

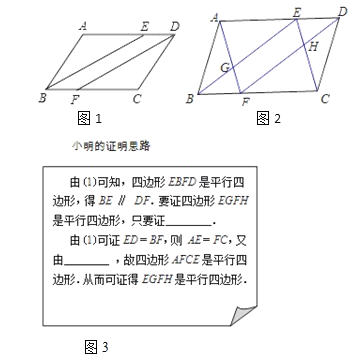
【题目】如图1，ABCD中，∠ABC、∠ADC的平分线分别交AD、BC于点E、F．

（1）求证：四边形EBFD是平行四边形；

（2）如图2，小明在完成（1）的证明后继续进行了探索．连接AF、CE，分别交BE、FD于点G、H，得到四边形EGFH．此时，他猜想四边形EGFH是平行四边形，请在框图（图3）中补全他的证明思路，再在答题纸上写出规范的证明过程．

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】

（1）由平行四边形的性质得出AD∥BC，∠ABC=∠ADC．AD=BC，由角平分线得出∠ABE=∠EBC=∠ADF=∠CDF．证出EB∥DF，即可得出结论；

（2）由平行四边形的性质得出BE∥DF，DE=BF，得出AE=CF，证出四边形AFCE是平行四边形，得出GF∥EH，即可证出四边形EGFH是平行四边形．

证明：在ABCD 中，AD∥BC，∠ABC=∠ADC．AD=BC．

∵BE 平分∠ABC，∴∠ABE=∠EBC=∠ABC．

∵DF 平分∠ADC，∴∠ADF=∠CDF=∠ADC．

∵∠ABC=∠ADC．

∴∠ABE=∠EBC=∠ADF=∠CDF．

∵AD∥BC，

∴∠AEB=∠EBC．

∴∠AEB=∠ADF．

∴EB∥DF．

∵ED∥BF，

∴四边形 EBFD 是平行四边形．

（2）①补全思路：GF∥EH，AE∥CF；

②理由如下：

∵四边形 EBFD 是平行四边形；

∴BE∥DF，DE=BF，

∴AE=CF，

又∵AE∥CF，

∴四边形 AFCE 是平行四边形，

∴GF∥EH，

∴四边形 EGFH 是平行四边形．