已知⊙O1和⊙O2相切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长是________.
分析:分别从⊙O
1和⊙O
2内切与外切去分析,根据切线的性质,利用勾股定理即可求得答案.
解答:
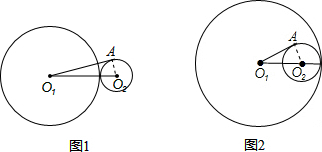
解:如图1,⊙O
1和⊙O
2外切,
连接O
2A;
∵⊙O
1和⊙O
2外切,
∴O
1O
2=3+1=4;
∵O
1A是⊙O
2的切线,
∴O
2A⊥O
1A,
在Rt△O
1O
2A中,O
1O
2=4,O
2A=1,
由勾股定理得:O
1A=

=

,
如图2,⊙O
1和⊙O
2内切,
连接O
2A,
∴O
1O
2=3-1=2;
∵O
1A是⊙O
2的切线,
∴O
2A⊥O
1A,
在Rt△O
1O
2A中,O
1O
2=2,O
2A=1,
由勾股定理得:O
1A=

=

.
∴O
1A的长是
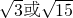
.
故答案为:

或

.
点评:此题考查了相切两圆的性质以及勾股定理.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

 解:如图1,⊙O1和⊙O2外切,
解:如图1,⊙O1和⊙O2外切, =
= ,
, =
= .
.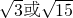 .
. 或
或 .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案