
【题目】如图,在ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF,CE.
求证:AF∥CE.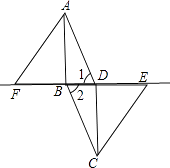
【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠1=∠2,
∵BF=DE,
∴BF+BD=DE+BD,
即DF=BE,
在△ADF和△CBE中,
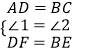 ,
,
∴△ADF≌△CBE(SAS),
∴∠AFD=∠CEB,
∴AF∥CE.
【解析】首先依据平行四边形的性质得出AD∥BC,AD=BC,然后依据平行线的性质可证明∠ADF=∠EBC,然后再利用等式的性质可证明DF=BE,接下来,再依据SAS证明△ADF≌△CBE,从而可得到∠AFD=∠CEB,最后,由平行线的判定进行证明即可.
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )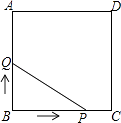
A.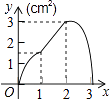
B.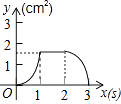
C.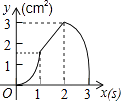
D.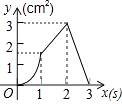
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
(1)试说明△PCM≌△QDM.
(2)当点P在点B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AC∥BE,∠MAC=40,∠D=50°,CH平分∠ACD,BH平分∠ABD,
(1)求∠EBH的角度
(2)求∠BHC的角度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.
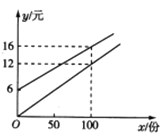
(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示数a,b,A、B两点之间的距离表示为![]() 。数轴上A、B两点之间的距离
。数轴上A、B两点之间的距离![]() 。
。
回答下列问题:
(1)数轴上表示-1和-4的两点之间的距离是 ;
(2)数轴上表示x和-1的两点A之和B之间的距离是 ,如果![]() =2,那么x的值是 ;
=2,那么x的值是 ;
(3) 若x表示一个有理数,且﹣1<x<3,则|x﹣3|+|x+1|= ;
(4)若x表示一个有理数,且|x﹣1|+|x+2|>3,则有理数x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com