
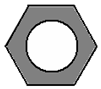
 如图,六角螺母的横截面是正六边形,它的每条边都相等,每个内角也都相等.求这个六边形的每一个内角的度数.
如图,六角螺母的横截面是正六边形,它的每条边都相等,每个内角也都相等.求这个六边形的每一个内角的度数.  同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
| x | … | -7 | -5 | -3 | -1 | 1 | 3 | 5 | … |
| y | … | -9 | -9 | -1 | 0 | -1 | -4 | -9 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20或16 | B. | 20 | C. | 16 | D. | 以上答案均不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12.用这块材料剪出一个矩形CDEF,其中,点D、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).设AE=x,矩形CDEF的面积为S.
一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12.用这块材料剪出一个矩形CDEF,其中,点D、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).设AE=x,矩形CDEF的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
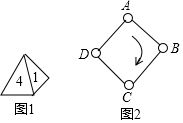 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
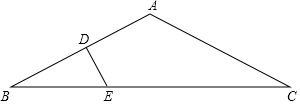 如图,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分线交AB于点D,交BC于点E,设△BDE的面积为S1,四边形ADEC的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.
如图,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分线交AB于点D,交BC于点E,设△BDE的面积为S1,四边形ADEC的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com