
如图,直线y=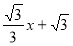 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点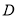 是劣弧AO上一动点(
是劣弧AO上一动点(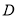 点与
点与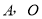 不重合).抛物线y=-
不重合).抛物线y=-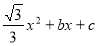 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,

(1)求抛物线的解析式及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,是︱PA—PC︱的值最大;若存在,求出点P的坐标;若不存在,请说明理由。
(3)连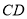 交
交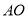 于点
于点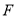 ,延长
,延长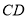 至
至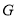 ,使
,使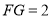 ,试探究当点
,试探究当点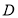 运动到何处时,直线
运动到何处时,直线 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.
(1)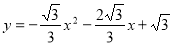 B(1,0)
B(1,0)
(2)P(-1,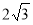 )
)
(3)当D运动到劣弧AO的中点时,直线AG与⊙M相切.证明见解析
【解析】
试题分析:(1)先求出A、C点坐标,再代入y=-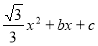 即可求出b、c的值,从而确定抛物线的解析式,由于点A、B关于抛物线的对称轴对称,从而可求出点B的坐标.
即可求出b、c的值,从而确定抛物线的解析式,由于点A、B关于抛物线的对称轴对称,从而可求出点B的坐标.
(2)连接BC并延长交抛物线对称轴于一点,这一点就是点P.
(3)当D运动到劣弧AO的中点时,直线AG与⊙M相切.
试题解析:(1)【解析】
由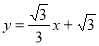 得A(-3,0),C(0, )
得A(-3,0),C(0, )
将其代入抛物线解析式得: 解得:
解得:
∴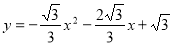
∵对称轴是x=-1
∴由对称性得B(1,0)
(2)【解析】
延长BC与对称轴的交点就是点P
由B(1,0),C(0,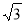 )求得直线BC解析式为:
)求得直线BC解析式为: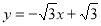
当x=-1时,y=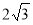
∴P(-1, 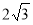 )
)
(3)结论:当D运动到劣弧AO的中点时,直线AG与⊙M相切.
证明:∵在RT△AOC中,tan∠CAO=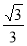 ,
,
∴∠CAO=30°,∠ACO=60°,
∵点D是劣弧AO的中点,
∴弧AD=弧OD
∴∠ACD=∠DCO=30°,
∴OF=OCtan30°=1,∠CF O=60°,
∴△AFG中,AF=3-1=2,∠AFG=∠CFO=60°,
∵FG=2,
∴△AFG为等边三角形,
∴∠GAF=60°,
∴∠CAG=30°+60°=90°,
∴AC⊥AG,
∴AG为⊙M的切线.
考点: 1. 二次函数综合题;2.直线与圆的位置关系.


科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十五讲练习卷(解析版) 题型:填空题
如图,△ABC的外接圆的圆心坐标为________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十三讲练习卷(解析版) 题型:选择题
某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行 小时到达B处,那么tan∠ABP=( )
小时到达B处,那么tan∠ABP=( )

A. B.2
B.2
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十七讲练习卷(解析版) 题型:选择题
为了解某校2 000名师生对我市 “三创”工作(创国家园林城市、国家卫生城市、全国文明城市)的知晓情况,从中随机抽取了100名师生进行问卷调查,这项调查中的样本是( )
A.2 000名师生对“三创”工作的知晓情况
B.从中抽取的100名师生
C.从中抽取的100名师生对“三创”工作的知晓情况
D.100
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十一讲练习卷(解析版) 题型:选择题
如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )

A.25° B.30° C.35° D.40°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市石岩公学九年级3月质量检测数学试卷(解析版) 题型:选择题
二次函数 的图象如图所示,则反比例函数
的图象如图所示,则反比例函数 与一次函数
与一次函数 在同一坐标系中的大致图象是( ).
在同一坐标系中的大致图象是( ).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市九年级3月联考数学试卷(解析版) 题型:填空题
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为____________米.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省云浮市九年级上学期期末考试数学试卷(解析版) 题型:解答题
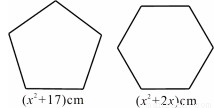
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(x2+17)cm,正六边形的边长为(x2+2x)cm(其中x>0)。求这两段铁丝的总长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com