
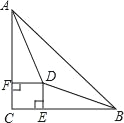
【题目】如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由(提示:可作DG⊥AB于点G)
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.
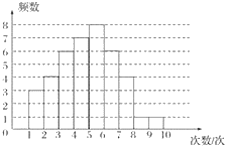
(1)求共抽取了多少名学生进行引体向上测试?
(2)试估计该校九年级学生引体向上次数不低于5次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有2位股东,20名工人、从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示.
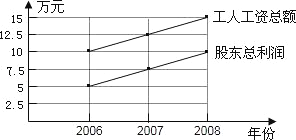
(1)填写下表:
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 | 5000 | ||
股东的平均利润/元 | 25000 |
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
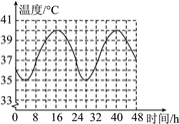
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是_____.
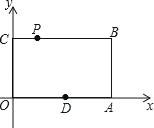
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国淡水资源短缺问题十分突出,已成为我国经济和社会可持续发展的重要制约因素,节约用水是各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区20户家庭的月用水量,结果如表所示:

(1)求这20户家庭月用水量的平均数、众数及中位数.
(2)政府为了鼓励节约用水,拟试行水价浮动政策.即设定每个家庭月基本用水量a(t),家庭月用水量不超过a(t)的部分按原价收费,超过a(t)的部分加倍收费.
①你认为以平均数作为该小区的家庭月基本用水量a(t)合理吗?为什么?(简述理由)
②你认为该小区的家庭月基本用水量a(t)为多少时较为合理?为什么?(简述理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com