
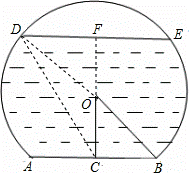
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=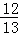 ,DE是水位线,DE∥AB.
,DE是水位线,DE∥AB.
(1)当水位线DE=4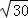 m时,求此时的水深;
m时,求此时的水深;
(2)若水位线以一定的速度下降,当水深8m时,求此时∠ACD的余切值.
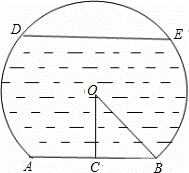
解:(1)延长CO交DE于点F,连接OD
∵OC⊥AB,OC过圆心,AB=24m,
∴BC= AB=12m.
AB=12m.
在Rt△BCO中,sin∠COB=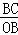 =
=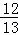 ,
,
∴OB=13mCO=5m.
∵DE∥AB,
∴∠ACD=∠CDE,∠DFO=∠BCO=90°.
又∵OF过圆心,
∴DF=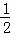 DE=
DE=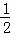 ×4
×4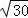 =2
=2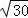 m.
m.
在Rt△DFO中,OF=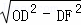 =
=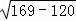 =7m,
=7m,
∴CF=CO+OF=12m,即当水位线DE=4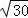 m时,此时的水深为12m;
m时,此时的水深为12m;
(2)若水位线以一定的速度下降,当水深8m时,即CF=8m,则OF=CF﹣OC=3m,
连接CD,在Rt△ODF中,DF=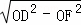 =
=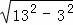 =4
=4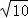 m.
m.
在Rt△CDF中,cot∠CDF=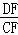 =
=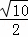 .
.
∵DE∥AB,
∴∠ACD=∠CDE,
∴cot∠ACD=cot∠CDF=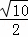 .
.
答:若水位线以一定的速度下降,当水深8m时,此时∠ACD的余切值为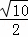 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为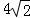 ,则a的值是( )
,则a的值是( )
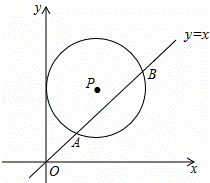
A. 4 B.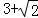 C.
C.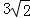 D.
D. 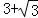
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
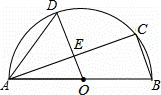
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
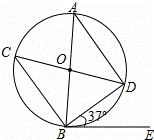
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com