
| ������ | �������ˣ� | Ƶ�� |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
���� ��1������A��������48����Ӧ��Ƶ����0.48���������������Ȼ�����ðٷֱȵ��������a��b��ֵ��
��2��������λ���Ķ��弴��ȷ����
��3������8000���Զ�Ӧ�İٷֱȼ�����⣮
��� �⣺��1����ȡ���������ǣ�48��0.48=100���ˣ���
��a=100��0.32=32��
b=100��0.10=10��
�ʴ�Ϊ32��10��
��2����ͬѧ�����ɼ�Ӧ��B�����Σ�
�ʴ��ǣ�B��
��3�������ɼ�Ϊ�����ѧ��������8000����0.48+0.32��=6400��������
�ʴ�Ϊ6400��
���� ���⿼���Ƶ���ֲ�ֱ��ͼ������������ͳ��ͼ��ȡ��Ϣ��������ͬʱ������λ����������n�����ݣ�����С�����������nΪ������λ���м���Ǹ���������λ�������nΪż����λ���м���������ƽ����������λ�����κ�һ�����ݣ���һ��������λ���ģ�����λ����һ��������������������


 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
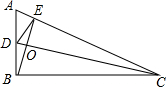 ��ͼ��D��E�ֱ��ǡ�ABC�ı�AB��AC�ϵĵ㣬BE��CD�ཻ�ڵ�O����AD•AB=AE•AC����OEC���ODB������Ϊʲô��
��ͼ��D��E�ֱ��ǡ�ABC�ı�AB��AC�ϵĵ㣬BE��CD�ཻ�ڵ�O����AD•AB=AE•AC����OEC���ODB������Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ӱ���ָ����Ӱڵ��˶� | B�� | վ�ڵ����ϵ��˵��˶� | ||
| C�� | ���ڻ���˯�� | D�� | ����ˮλ�������½� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com