
如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
(1)求证:PB为⊙O的切线;(4分)
(2)若OC=1,AB=2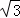 ,求图中阴影部分的面积S;(3分)
,求图中阴影部分的面积S;(3分)
(3)若 ,求sinE的值.(3分)
,求sinE的值.(3分)

解:(1)证明:连接OA
∵PA为⊙O的切线,∴∠PAO=90°,
∵OA=OB,OP⊥AB于C,
∴BC=CA,PB=PA,∴△PBO≌△PAO
∴∠PBO=∠PAO=90°,∴PB为⊙O的切线.
(2) ∵OP⊥AB,∴BC=AC=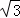 ,
,
在Rt△OBC中,由tan∠BOC=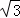 知,∠BOC=60°,则∠BOA=120°,OB=2,
知,∠BOC=60°,则∠BOA=120°,OB=2,
BP=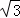 OB=2
OB=2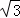
∴S=S四边形OBPA﹣S扇形OBA=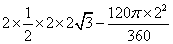 =
=
(3) 解法1:连接AD,∵BD是直径,∠BAD=90°
由(1)知∠BCO=90°,∴AD∥OP,
∴△ADE∽△POE,∴EA/EP=AD/OP
由AD∥OC得AD=2OC,
∵tan∠ABE=1/2 , ∴OC/BC=1/2,
设OC=t,则BC=2t,AD=2t,
由△PBC∽△BOC,得PC=2BC=4t,OP=5t
∴EA/EP=AD/OP=2/5,…………………(9分)
可设EA=2m,EP=5m,则PA=3m
∵PA=PB∴PB=3m∴sinE=PB/EP=3/5.
解法2:连接AD,则∠BAD=90°,
由(1)知∠BCO=90°,∵由AD∥OC,∴AD=2OC
∵tan∠ABE=1/2,∴OC/BC=1/2,设OC=t,BC=2t,AB=4t
由△PBC∽△BOC,得PC=2BC=4t,∴PA=PB=2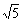 t
t
过A作AF⊥PB于F,则AF·PB=AB·PC∴AF=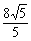 t,
t,
由勾股定理得PF= t,
t,
∴sinE=sin∠FAP=PF/PA=3/5.


科目:初中数学 来源: 题型:
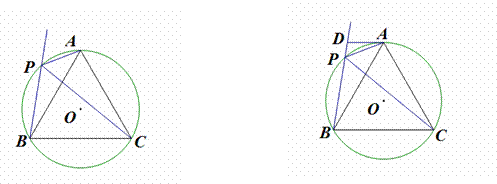
如图12-1,⊙O是等边三角形ABC的外接圆,点 P是 ⊙O 上一点,连结CP、AP,作射线BP.
(1)求证:PC平分∠APB;
(2)试猜想线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)如图12-2,过点A做⊙O的切线交射线BP于点D.若AD=2,PD=1,求⊙O的半径.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
餐桌边的一蔬一饭,舌尖上的一饮一酌,实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,500亿用科学记数法表示为
查看答案和解析>>
科目:初中数学 来源: 题型:
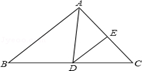
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE等于( )
A.45° B.54° C.40° D.50°
C.40° D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
某同学春节期间将自己的压岁钱800元,存入银行.十一放假取出350元买了礼物去看爷爷,母亲节时他又取出100元给妈妈买了礼物,则存上存入、支出情况显示为( )
A.+800,+350,﹣100 B.+800,+350, +100
+100
C.+800,﹣350,﹣100 D.﹣800,﹣350,+100
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com