
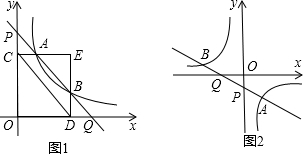
���� ��1����ȷ������A��B���꣬�����ó�AE��CE��BE��DE�������߶�Ӧ�ɱ������н���ȵó����ۣ�
��2����ȷ����ֱ��PQ����ʽ�������ó�P��Q�����꣬�������ľ��빫ʽ��⼴�ɵó����ۣ�
��3��ͬ��2���ķ������ɵó����ۣ�
��� �⣺��1���ߵ�A��B��˫����y=$\frac{k}{x}$��k��0����һ����һ֧���������㣬���ǵĺ�����ֱ�Ϊa��b��
��A��a��$\frac{k}{a}$����B��b��$\frac{k}{b}$����
��AC=a��CE=b��BD=$\frac{k}{b}$��DE=$\frac{k}{a}$��
��AE=CE-AC=b-a��BE=DE-BD=$\frac{k}{a}-\frac{k}{b}=\frac{k}{ab}��b-a��$��
��$\frac{AE}{CE}=\frac{b-a}{b}$��$\frac{BE}{DE}=\frac{\frac{k}{ab}��b-a��}{\frac{k}{a}}$��
��$\frac{AE}{CE}=\frac{BE}{DE}$��
�ߡ�AEB=��CED=90�㣬
���EAB�ס�ECD��
��2����ֱ��PQ����ʽΪy=k'x+b'��
��A��a��$\frac{k}{a}$����B��b��$\frac{k}{b}$������ֱ��PQ�ϣ�
��$\left\{\begin{array}{l}{ak'+b'=\frac{k}{a}}\\{bk'+b'=\frac{k}{b}}\end{array}\right.$��
��$\left\{\begin{array}{l}{k'=-\frac{k}{ab}}\\{b'=\frac{k}{ab}��a+b��}\end{array}\right.$
��ֱ��PQ����ʽΪy=-$\frac{k}{ab}$x+$\frac{k}{ab}��a+b��$��
��P��0��$\frac{k}{ab}��a+b��$��Q��a+b��0����
��A��a��$\frac{k}{a}$����B��b��$\frac{k}{b}$����
��AP2=a2+[$\frac{k}{ab}��a+b��$-$\frac{k}{a}$]2=a2+��$\frac{k}{b}$��2��
BQ2=��a+b-b��2+��0-$\frac{k}{b}$��2=a2+��$\frac{k}{b}$��2��
��PA=BQ��
��3��AP=BQ��BP=AQ��
���ɣ�AP=BQ��BP=AQ��
��A��a��$\frac{k}{a}$����B��b��$\frac{k}{b}$����
��ֱ��AB����ʽΪy=-$\frac{k}{ab}$x+$\frac{k}{ab}��a+b��$��
��P��0��$\frac{k}{ab}��a+b��$��Q��a+b��0����
��A��a��$\frac{k}{a}$����B��b��$\frac{k}{b}$����
��AP2=a2+[$\frac{k}{ab}��a+b��$-$\frac{k}{a}$]2=a2+��$\frac{k}{b}$��2��
BQ2=��a+b-b��2+��0-$\frac{k}{b}$��2=a2+��$\frac{k}{b}$��2��
��AP2=BQ2��
��AP=BQ��
��BP=AQ��
���� �����Ƿ����������ۺ��⣬��Ҫ�����˷��������������ʣ����������ε��ж�������ϵ�У������ľ��빫ʽ���Ȿ��Ĺؼ����ж�PA=BQ��Ҳ�ǽⱾ����ѵ㣬��һ���е��Ѷȵ��п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 361 | B�� | 231 | C�� | 230 | D�� | 260 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ijУ��180�����б�ҵ��������һ�������������飬���Ƴ�Ƶ���ֲ�ֱ��ͼ������������ͼ��ʾ������γ��������������ݵ���λ��Ϊx������ͼ�е���Ϣ�ж�x��ȡֵ��Χ�ǣ�������
ijУ��180�����б�ҵ��������һ�������������飬���Ƴ�Ƶ���ֲ�ֱ��ͼ������������ͼ��ʾ������γ��������������ݵ���λ��Ϊx������ͼ�е���Ϣ�ж�x��ȡֵ��Χ�ǣ�������| A�� | 0��x��4.3 | B�� | 4.3��x��4.6 | C�� | 4.6��x��4.9 | D�� | 4.9��x��5.2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com