练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在实数：3.1415926，，1.010010001…（每两个1之间依次多一个0），3.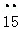，中，有理数的个数为（　　）

    　 A． 1 B． 2 C． 3 D． 4


    C．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列函数中，当x﹥0时，y随x的增大而减小的是：

    A.y=x+1               B.        C.            D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD=3，另两边与反比例函数y=（k≠0）的图象分别相交于点E，F，且DE=2．过点E作EH⊥x轴于点H，过点F作FG⊥EH于点G．回答下面的问题：

    ①该反比例函数的解析式是什么？

    ②当四边形AEGF为正方形时，点F的坐标是多少？

    （1）阅读合作学习内容，请解答其中的问题；

    （2）小亮进一步研究四边形AEGF的特征后提出问题：“当AE＞EG时，矩形AEGF与矩形DOHE能否全等？能否相似？”

    针对小亮提出的问题，请你判断这两个矩形能否全等？直接写出结论即可；这两个矩形能否相似？若能相似，求出相似比；若不能相似，试说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）将抛物线y1=2x2向右平移2个单位，得到抛物线y2的图象，则y2=2（x﹣2）2或2x2﹣8x+8；

    （2）如图，P是抛物线y2对称轴上的一个动点，直线x=t平行于y轴，分别与直线y=x、抛物线y2交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则

    查看答案和解析>>

    科目：初中数学 来源： 题型：


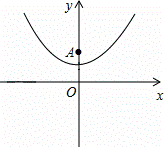
    已知抛物线y=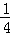x2+1（如图所示）．

    （1）填空：抛物线的顶点坐标是（0，1），对称轴是x=0（或y轴）；

    （2）已知y轴上一点A（0，2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；

    （3）在（2）的条件下，点M在直线AP上．在平面内是否存在点N，使四边形OAMN为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某种商品的进价为300元，出售标价为440元，后来由于该商品积压，商店准备打折销售，但要保证利润率为10%，则商店可打（　　）

    　 A． 6折 B． 6.5折 C． 7.3折 D． 7.5折

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知∠AOB=α，∠BOC=β，（α＞β），且OD，OE分别为∠AOB，∠BOC的角平分线，则∠DOE的度数为　　　　　　（结果用α，β的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于等边三角形，下列说法中错误的是(     )

          A．等边三角形中，各边都相等

          B．等边三角形是特殊的等腰三角形

          C．三个角都等于60°的三角形是等边三角形

          D．有一个角为60°的等腰三角形不是等边三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知AE∥BC，AE平分∠DAC．

    求证：AB=AC．

    　

    查看答案和解析>>

    同步练习册答案