
【题目】如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
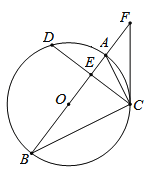
(1)求证:CF是⊙O的切线.
(2)若AC=4,tan∠ACD![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用圆周角定理以及等腰三角形的性质得出∠OCF=90°,进而得出答案;
(2)利用垂径定理推论得出![]() ,进而得出BC的长,再利用勾股定理求出即可.
,进而得出BC的长,再利用勾股定理求出即可.
试题解析:(1)连接CO,
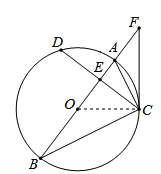
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠ACO+∠OCB=90°,
∵OB=CO,
∴∠B=∠OCB,
∵∠FCA=∠B,
∴∠BCO=∠ACF,
∴∠OCA+∠ACF=90°,
即∠OCF=90°,
∴CF是⊙O的切线;
(2)∵直径AB平分弦CD,
∴AB⊥DC,
∴![]() ,
,
∵AC=4,tan∠ACD=![]() ,
,
∴tan∠B=tan∠ACD=![]() ,
,
∴![]()
∴BC=8,
∴在Rt△ABC中,
AB=![]()
则⊙O的半径为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 两组对边分别相等的四边形是平行四边形
B. 圆内最大的弦是直径
C. 有三条边对应相等的两个三角形全等
D. 长度相等的弧是等弧
查看答案和解析>>
科目:初中数学 来源: 题型:
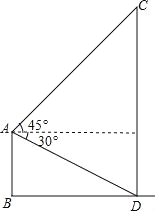
【题目】如图,平地上一个建筑物AB与铁塔CD相距60m,在建筑物的顶部测得铁塔底部的俯角为30°,测得铁塔顶部的仰角为45°,求铁塔的高度(![]() 取1.732,精确到1m).
取1.732,精确到1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆的周长C=2πR中,常量与变量分别是( )
A.2是常量,C、π、R是变量
B.2π是常量,C、R是变量
C.C、2是常量,R是变量
D.2是常量,C、R是变量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(8,3)向上平移6个单位长度,下列说法正确的是( )
A. 点P的横坐标加6,纵坐标不变
B. 点P的纵坐标加6,横坐标不变
C. 点P的横坐标减6,纵坐标不变
D. 点P的纵坐标减6,横坐标不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com