
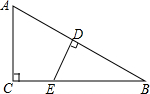
 在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.
在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| -11+3=-8 | -39+(-21)=-60 | (-2015)+2014=-1 |
| -3-(-1.2)=-1.8 | (-$\frac{3}{4}$)-(+$\frac{1}{4}$)=-1 | (0.04)×(-0.05)=-0.002 |
| (-$\frac{2}{3}$)×(-1$\frac{1}{2}$)=1 | (-32)÷(-8)=4 | (-2$\frac{1}{12}$)÷1.25=-$1\frac{2}{3}$ |
| (-3)4=81 | (-$\frac{1}{2}$3)=-$\frac{1}{8}$ | -$\frac{{2}^{2}}{7}$=-$\frac{4}{7}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
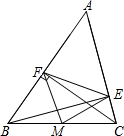 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,连接MF、ME.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,连接MF、ME.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:
如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p=0,q=0 | B. | p=-3,q=-1 | C. | p=3,q=1 | D. | p=-3,q=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
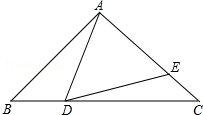 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com