
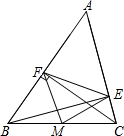
 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,连接MF、ME.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,连接MF、ME.分析 (1)根据CF⊥AB,BE⊥AC,△BCE和△BCF是Rt△,再根据M为BC的中点,由直角三角形的性质,斜边上的中线等于斜边的一半,即可得出ME=MF;
(2)根据ME=MF=BM=CM,可得∠MBF=∠MFB,∠MEC=MCE,由∠ABC=50°,∠ACB=60°,即可求得∠EMF的度数.
解答 解:(1)证明:∵CF⊥AB,BE⊥AC,
∴△BCE和△BCF是Rt△,
∵M为BC的中点,
∴MF=BM=CM,ME=BM=CM,
∴ME=MF;
(2)∵ME=MF=BM=CM,
∴∠MBF=∠MFB,∠MEC=MCE,
∵∠ABC=50°,∠ACB=60°,
∴∠BMF=80°∠CME=60°,
∴∠EMF=180°-80°-60°=40°,
∴∠FME的度数为40°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半以及等腰三角形的判定和性质,熟练掌握直角三角形的性质是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
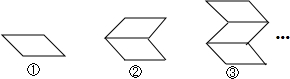
| 图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
| 火柴棒的根数 | 4 | 7 | 10 | 13 | 16 | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24 | B. | 48 | C. | 24或8$\sqrt{5}$ | D. | 8$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
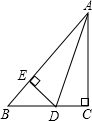 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BC=9,BE=3,则△BDE的周长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BC=9,BE=3,则△BDE的周长为( )| A. | 15 | B. | 12 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
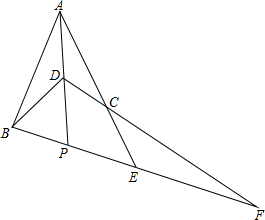 如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB=∠PDC.
如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB=∠PDC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
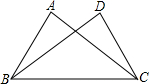 如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )| A. | 3cm | B. | 5cm | C. | 6cm | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com