
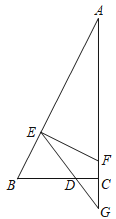
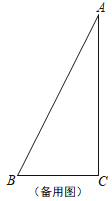
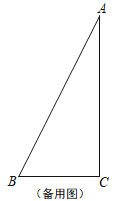
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)请探究线段AF与FG的倍数关系,并证明你的结论。
(3)设FG=x,△EFG的面积为y,求y关于x的函数解析式,并直接写出x的取值范围;
【答案】(1)见解析;(2)AF=3 FG ;(3)![]()
【解析】分析:(1)先证明∠A=∠2,然后利用相似三角形的判定方法即可得到结论;
(2)证明△EFG∽△AEG即可得解.
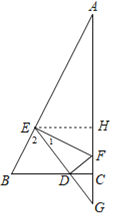
(3)作EH⊥AF于点H,如图1,利用勾股定理计算出AB=2![]() ,利用△EFG∽△AEG得到
,利用△EFG∽△AEG得到![]() ,再证明Rt△AEF∽Rt△ACB得到
,再证明Rt△AEF∽Rt△ACB得到![]() ,所以
,所以![]() ,则EG=2x,AG=4x,AF=3x,EF=
,则EG=2x,AG=4x,AF=3x,EF=![]() x,AE=
x,AE=![]() x,接着利用相似比表示出EH=
x,接着利用相似比表示出EH=![]() x,AH=
x,AH=![]() x,然后根据三角形面积公式表示出y与x的关系,最后利用CF=4-3x可确定x的范围;
x,然后根据三角形面积公式表示出y与x的关系,最后利用CF=4-3x可确定x的范围;
详解:(1)证明:∵ED=BD,
∴∠B=∠2,
∵∠ACB=90°,
∴∠B+∠A=90°.
∵EF⊥AB,
∴∠BEF=90°,
∴∠1+∠2=90°,
∴∠A=∠2,
∵∠EGF=∠AGE,
∴△EFG∽△AEG;
(2)答:AF=3 FG
证明:作EH⊥AF于点H.
∵ 在Rt△ABC中,∠ACB=90°,BC=2,AC=4,
∴ ![]() .
.
∴ 在Rt△AEF中,∠AEF=90°,![]() .
.
∵ △EFG∽△AEG,
∴ ![]() .
.
∴ EG=2 FG,
∴AG=2 EG=4 FG
∴AF=3 FG
(3)∵ FG=x,
∴ EG=2x,AG=4x.
∴ AF=3x.
∵ EH⊥AF,
∴ ∠AHE=∠EHF=90°.
∴ ∠EFA+∠FEH=90°.
∵ ∠AEF=90°,
∴ ∠A+∠EFA=90°.
∴ ∠A=∠FEH.
∴ tanA =tan∠FEH.
∴ 在Rt△EHF中,∠EHF=90°,![]() .
.
∴ EH=2HF.
∵ 在Rt△AEH中,∠AHE=90°,![]() .
.
∴ AH=2EH.
∴ AH=4HF.
∴ AF=5HF.
∴ HF=![]() .
.
∴ ![]() .
.
∴ ![]() .
.
x的取值范围![]() .
.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的大括号里:
1, —5, ![]() , —4.2, 0,
, —4.2, 0, ![]() , 10,—
, 10,—![]() ,
,
整数:{ … }
非负整数:{ … }
分数:{ … }
负分数:{ … }
有理数:{ … }
非负有理数:{ … }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约![]() 亿
亿![]() (占总用水量的
(占总用水量的![]() ),工业用水量约为
),工业用水量约为![]() 亿
亿![]() ,生活用水量具体见下表.
,生活用水量具体见下表.
2019-2017年全国生活用水量表(单位:亿![]() )
)
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
用水量 |
|
|
|
|
|
|
|
|
|
(1)2017年全国总用水量约为 亿![]() ,其他用水约为 亿
,其他用水约为 亿![]() .
.
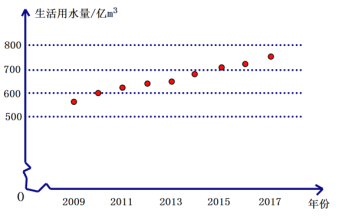
(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图图形:
它们是按一定规律排列的:
(1)依照此规律,第8个图形共有__枚五角星.
(2)用代数式表示第n个图形共有___枚五角星
(3)第99个图形共有多少枚五角星?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述正确的是( )
A. 符号不同的两个数是互为相反数
B. 一个有理数的相反数一定是负有理数
C. 2![]() 与2.75都是﹣
与2.75都是﹣![]() 的相反数
的相反数
D. 0没有相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
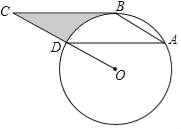
【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4![]() .
.
(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com