
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.

(1)求反比例函数和一次函数的解析式;
(2)求△![]() 的面积;
的面积;
【答案】(1)反比例函数的解析式为 y=-![]() ,一次函数的解析式为y=-x-2.(2)6.
,一次函数的解析式为y=-x-2.(2)6.
【解析】
(1)因为A(-4,n)、B(2,-4)是一次函数y=kx+b的图象与反比例函数![]() 的图象的两个交点,利用待定系数法,将点B(2,-4)代入反比例函数关系式求出k的值,再将A的横坐标代入,求出A的纵坐标,然后将A、B点的坐标代入一次函数y=kx+b,组成二元一次方程组,求出一次函数的关系式.
的图象的两个交点,利用待定系数法,将点B(2,-4)代入反比例函数关系式求出k的值,再将A的横坐标代入,求出A的纵坐标,然后将A、B点的坐标代入一次函数y=kx+b,组成二元一次方程组,求出一次函数的关系式.
(2)求出交点C的坐标,S△AOB=S△AOC+S△COB.
(1)把B(2,-4)代入反比例函数![]() ,
,
得到:-4=![]() ,解得m=-8.
,解得m=-8.
故所求反比例函数关系式为:y= -![]()
∵点A(-4,n)在反比例函数的图象上
∴n=![]() ,n=2
,n=2
∴点A的坐标为(-4,2)
由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴![]() ,
,
解得![]() .
.
∴反比例函数的解析式为 y=-![]() ,
,
一次函数的解析式为y=-x-2.
(2)根据(1)中的直线的解析式y=-x-2.且直线与x轴相交于点C,则令y=0
则x=-2,
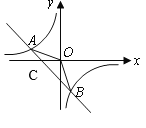
即直线与x轴的交点C的坐标是(-2,0)
∴S△AOB=S△AOC+S△COB=![]() ×2×2+
×2×2+![]() ×2×4=6.
×2×4=6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E,F,G,H分别是OA,OB,OC,OD的中点,则正方形EFGH与正方形ABCD的面积比是( )
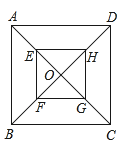
A. 1:6B. 1:5C. 1:4D. 1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(-3,-6)的抛物线![]() 经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程
经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程![]() 的两根为﹣5和﹣1,其中正确的有( )
的两根为﹣5和﹣1,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
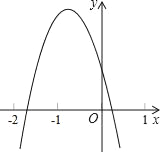
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com