
【题目】如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si39°≈0.63,cos39°≈0.78,tan39°≈0.81.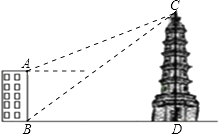
【答案】解:过点A作AE⊥CD于点E,
由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米
设大楼与塔之间的距离BD的长为x米,则AE=BD=x米,
∵在Rt△BCD中,tan∠CBD= ![]() ,
,
∴CD=BD tan 39°≈0.81x,
∵在Rt△ACE中,tan∠CAE= ![]() ,
,
∴CE=AE×tan 22°≈0.4x,
∵CD﹣CE=DE,
∴0.81x﹣0.4x=16,
解得x≈39.0,
即BD=39.0(米),
∴CD=0.81×39.0=31.6(米),
答:塔高CD是31.6米.
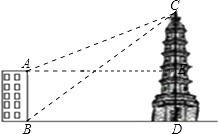
【解析】过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用x表示出CD和CE=AE,利用CD﹣CE=DE得到有关x的方程,求得x的值即可.
【考点精析】根据题目的已知条件,利用关于仰角俯角问题的相关知识可以得到问题的答案,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数 ![]() (m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;
(3)若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1 , y1),M2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
(1)S△ABC=;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为底边的等腰△ABP,使该三角形的面积等于△ABC的面积,并简要说明点P的位置是如何找到的(不要求证明) . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式;
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE= ![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,给出下列结论:
,给出下列结论:
①当![]() 时,
时,![]() ;
;
②![]() 为
为![]() 的平分线;
的平分线;
③与![]() 相等的角有三个;
相等的角有三个;
④![]() .
.
其中正确的结论为

A. ①②④ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
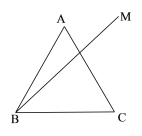
【题目】如图,等边△ABC中,BM是ABC内部的一条射线,且![]() ,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
(1)依题意补全图形;
(2)若ABM ,求BDC 的大小(用含的式子表示);
(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需要将方向调整到与出发时一致,则方向的调整应为( )
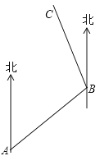
A.左转80°B.右转80°C.左转100°D.右转100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com