
【题目】已知二次函数![]() (
(![]() 是常数).
是常数).
(1)、求证:不论![]() 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)、把该函数的图象沿![]() 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与![]() 轴只有一个公共点?
轴只有一个公共点?
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.
(1)a= ,c= ;
(2)如图所示,在(1)的条件下,若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB,则b= ;
(3)在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= ,最小值为 ;
(4)在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C是数轴上三点,O为原点,点C对应的数为3,BC=2,AB=6.
(1)求点A,B对应的数;
(2)动点M,N分别同时从AC出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动.P为AM的中点,Q在CN上,且CQ=![]() CN,设运动时间为t(t > 0).
CN,设运动时间为t(t > 0).
①求点P,Q对应的数(用含t的式子表示);
②t为何值时OP=BQ.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口
袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随
机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1= ______ ;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为 ______ .
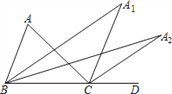
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由
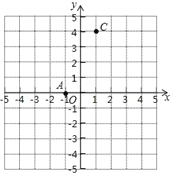
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽查了10名同学的期末成绩,以80分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,﹣3,+12,﹣7,﹣10,﹣4,﹣8,+1,0,+10.这10名同学的平均成绩是__分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com