
【题目】如图,已知点A,B,C是数轴上三点,O为原点,点C对应的数为3,BC=2,AB=6.
(1)求点A,B对应的数;
(2)动点M,N分别同时从AC出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动.P为AM的中点,Q在CN上,且CQ=![]() CN,设运动时间为t(t > 0).
CN,设运动时间为t(t > 0).
①求点P,Q对应的数(用含t的式子表示);
②t为何值时OP=BQ.
![]()
【答案】(1)-5,1;(2)①点P对应的数为![]() ,点Q对应的数为
,点Q对应的数为![]() ,②
,②![]() 或
或![]()
【解析】试题分析:(1)根据点B对应的数为1,AC=6,BC=2,得出点A对应的数是1-6=-5,点B对应的数是3-2=1.
(2) ①根据动点M、N分别同时从A、C出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动,表示出移动的距离,即可得出对应的数;②分两种情况讨论:当点P与点Q在原点两侧时和当点P与点Q在同侧时,根据OP=BQ,分别列出方程,求出t的值即可.
试题解析:
(1)∵点C对应的数为3,BC=2,
∴点B对应的数为3-2=1,
∵AB=6,
∴点A对应的数为1-6=-5.
(2)①∵动点M,N分别同时从A、C出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动,且运动时间为t
∴AM=3t,CN=t
∵P为AM的中点,Q在CN上,且CQ=![]() CN,
CN,
∴AP=![]() ,CQ=
,CQ=![]()
∵点A对应的数为-5,点C对应的数为3
∴点P对应的数为![]() ,点Q对应的数为
,点Q对应的数为![]()
②∵OP=BQ.
∴![]()
解得:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
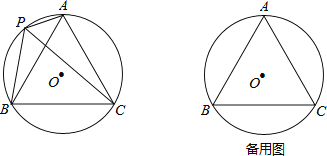
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状: ;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于![]() 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校开展的“厉行节约,你我有责”活动中,七年级某班对学生7天内收集饮料瓶的情况统计如下(单位:个):76,90,64,100,84,64,73.则这组数据的众数和中位数分别是( )
A.64,100 B.64,76 C.76,64 D.64,84
查看答案和解析>>
科目:初中数学 来源: 题型:
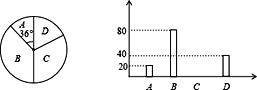
【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A、上网时间小时;B、1小时<上网时间小时;C、4小时<上网时间小时;D、上网时间>7小时.统计结果制成了如图统计图:
(1)参加调查的学生有 人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数).
是常数).
(1)、求证:不论![]() 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)、把该函数的图象沿![]() 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与![]() 轴只有一个公共点?
轴只有一个公共点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com