
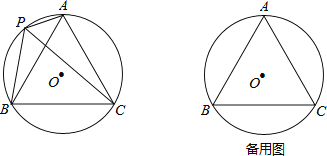
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状: ;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于![]() 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
【答案】(1)、等边三角形;(2)、CP=BP+AP;证明过程见解析;(3)、当点P为![]() 的中点时,四边形APBC的面积最大,最大值为
的中点时,四边形APBC的面积最大,最大值为![]() .
.
【解析】
试题分析:(1)、根据三角形的判定得出等边三角形;(2)、在PC上截取PD=AP,得出△APD是等边三角形,然后证明△APB和△ADC全等,从而得出BP=CD,然后得出答案;(3)、将四边形的面积转化成△ABP和△ABC的面积之和,然后根据两个三角形同底,要使面积最大,则就需要满足高最大,则当CP是直径时最大.
试题解析:(1)、△ABC是等边三角形
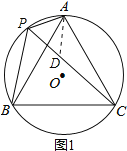
(2)、在PC上截取PD=AP,如图1, 又∵∠APC=60°,∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°. 又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,
在△APB和△ADC中,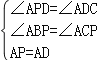 ,∴△APB≌△ADC(AAS), ∴BP=CD,又∵PD=AP, ∴CP=BP+AP
,∴△APB≌△ADC(AAS), ∴BP=CD,又∵PD=AP, ∴CP=BP+AP
(3)、当点P为![]() 的中点时,四边形APBC的面积最大.
的中点时,四边形APBC的面积最大.
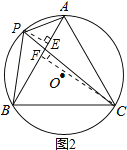
理由如下,如图2,过点P作PE⊥AB,垂足为E. 过点C作CF⊥AB,垂足为F.
∵S△APE=![]() ABPE,S△ABC=
ABPE,S△ABC=![]() ABCF,∴S四边形APBC=
ABCF,∴S四边形APBC=![]() AB(PE+CF),
AB(PE+CF),
当点P为![]() 的中点时,PE+CF=PC,PC为⊙O的直径, ∴此时四边形APBC的面积最大.又∵⊙O的半径为1,
的中点时,PE+CF=PC,PC为⊙O的直径, ∴此时四边形APBC的面积最大.又∵⊙O的半径为1,
∴其内接正三角形的边长AB=![]() , ∴S四边形APBC=
, ∴S四边形APBC=![]() ×2×
×2×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
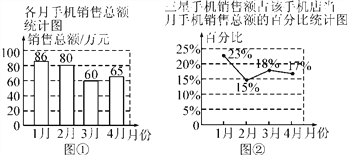
A. 4月份三星手机销售额为65万元
B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.
(1)a= ,c= ;
(2)如图所示,在(1)的条件下,若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB,则b= ;
(3)在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= ,最小值为 ;
(4)在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
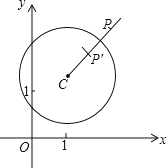
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1,![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C是数轴上三点,O为原点,点C对应的数为3,BC=2,AB=6.
(1)求点A,B对应的数;
(2)动点M,N分别同时从AC出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动.P为AM的中点,Q在CN上,且CQ=![]() CN,设运动时间为t(t > 0).
CN,设运动时间为t(t > 0).
①求点P,Q对应的数(用含t的式子表示);
②t为何值时OP=BQ.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
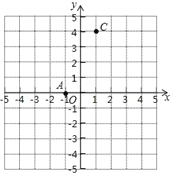
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com