
����Ŀ����ͼ����������A���ʾ��a��B���ʾ��b��C���ʾ��c����a��c����|a+3|+��c��9��2=0��
��1��a=�� ����c=�� ����
��2����ͼ��ʾ���ڣ�1���������£�����A���B֮��ľ����ʾΪAB=|a��b|����B���C֮��ľ����ʾΪBC=|b��c|����B�ڵ�A��C֮�䣬������BC=2AB����b=�� ����
��3���ڣ�1����2���������£�����PΪ������һ���㣬���Ӧ����Ϊx��������ʽ|x��a|+|x��b|+|x��c|ȡ����Сֵʱ����ʱx=�� ������СֵΪ�� ����
��4���ڣ�1����2���������£����ڵ�B����һ���壬һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�C����2����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt���룩�����ʾ���ס�����С��֮��ľ���d����t�Ĵ���ʽ��ʾ����
��![]()
���𰸡���1��a=��3��c=9��
��2��b=1��
��3����x=b=1ʱ����СֵΪ12��
��4����t������4�루�����Ϊ0��t��4��4����ǰ����d=12��t��
��t����4�루�����Ϊt��4��4���Ժ�d=3t��4��
�������������������1�����ݷǸ������������a=��3��c=9����2������BC=2AB��|c��b|=2|b��a|������������b��������3����P���B�غ�ʱ������x=bʱ��|x��a|+|x��b|+|x��c|ȡ����Сֵ����4���ֵ�0��t��4ʱ����t��4ʱ����ʾ���ס�����С��֮��ľ���d���ɣ�
���������
��1����|a+3|+��c��9��2=0��
��a+3=0��c��9=0��
��ã�a=��3��c=9��
��2�������ϵ�B��ʾ����Ϊb��
��BC=2AB��
��|c��b|=2|b��a|��
��9��b=2[b������3��]
��ã�b=1��
��3����x=b=1ʱ��
|x��a|+|x��b|+|x��c|=|x������3��|+|x��1|+|x��9|=12,Ϊ��Сֵ��
��4����t������4�루�����Ϊ0��t��4��4����ǰ����d=12��t��
��t����4�루�����Ϊt��4��4���Ժ�d=3t��4��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() x2+bx��2��x�ύ��A��B���㣬 ��y�ύ��C�㣬��A��һ1��0����
x2+bx��2��x�ύ��A��B���㣬 ��y�ύ��C�㣬��A��һ1��0����
���������ߵĽ���ʽ������D�����ꣻ
���жϡ�ABC����״��֤����Ľ��ۣ�
�ǵ�M(m��0)��x���ϵ�һ�����㣬��CM+DM��ֵ��Сʱ����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڿ���ѧϰʱ��������һ�����⣺
���壺������κ���![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �����������������Ϊ����ת��������
�����������������Ϊ����ת��������
����![]() ������ת��������
������ת��������
С��������˼���ģ��ɺ���![]() ��֪��
��֪��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �����
�����![]() ��
��![]() ��
��![]() ������ȷ���������������ת��������
������ȷ���������������ת��������
��ο�С���ķ�������������⣺
��1��ֱ��д������![]() ������ת��������
������ת��������
��2��������![]() ��
��![]() ��Ϊ����ת����������
��Ϊ����ת����������![]() ��ֵ��
��ֵ��
��3����֪����![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�A��B���㣨A��B����ߣ�����
�ύ�ڵ�A��B���㣨A��B����ߣ�����![]() �ύ�ڵ�C����A��B��C����ԭ��ĶԳƵ�ֱ���A1��B1��C1����֤��������A1��B1��C1�Ķ��κ����뺯��
�ύ�ڵ�C����A��B��C����ԭ��ĶԳƵ�ֱ���A1��B1��C1����֤��������A1��B1��C1�Ķ��κ����뺯��![]() ��Ϊ����ת��������
��Ϊ����ת��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
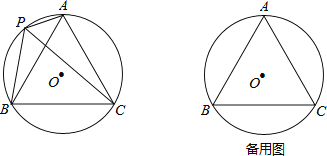
����Ŀ����ͼ����O�İ뾶Ϊ1��A��P��B��C����O�ϵ��ĸ��㣬��APC=��CPB=60����
��1���ж���ABC����״�� ��
��2����̽���߶�PA��PB��PC֮���������ϵ����֤����Ľ��ۣ�
��3������Pλ��![]() ��ʲôλ��ʱ���ı���APBC�������������������
��ʲôλ��ʱ���ı���APBC�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����У�һ�����ӿ���6�ˣ�����ͼ��ʾ�����ְڷŷ�ʽ��

��1������n������ʱ�����ְڷŷ�ʽ�����������ˣ�
��2��һ���������Ҫ�Ӵ�98λ�˿�ͬ�Ͳͣ�������ֻ��25�������IJ���.��������������ľ����������ѡ�����ַ�ʽ���ڷŲ�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��![]() �dz�������
�dz�������
(1)����֤������![]() Ϊ��ֵ���ú�����ͼ����x��û�й����㣻
Ϊ��ֵ���ú�����ͼ����x��û�й����㣻
(2)���Ѹú�����ͼ����![]() ������ƽ�ƶ��ٸ���λ���Ⱥõ��ĺ�����ͼ����
������ƽ�ƶ��ٸ���λ���Ⱥõ��ĺ�����ͼ����![]() ��ֻ��һ�������㣿
��ֻ��һ�������㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com