
【题目】(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .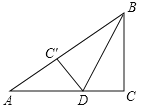
【答案】6cm2
【解析】
先根据勾股定理得到AB=10cm,再根据折叠的性质得到DC=DC′,BC=BC′=6cm,则AC′=4cm,设DC=xcm,在Rt△ADC′中根据勾股定理列方程求得x的值,然后根据三角形的面积公式计算即可.
∵∠C=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∵将△BCD沿BD折叠,使点C落在AB边的C′点,
∴△BCD≌△BC′D,
∴∠C=∠BC′D=90°,DC=DC′,BC=BC′=6cm,
∴AC′=AB-BC′=4cm,
设DC=xcm,则AD=(8-x)cm,
在Rt△ADC′中,AD2=AC′2+C′D2,
即(8-x)2=x2+42,解得x=3,
∵∠AC′D=90°,
∴△ADC′的面积═![]() ×AC′×C′D=
×AC′×C′D=![]() ×4×3=6(cm2).
×4×3=6(cm2).


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,PA是⊙O的切线,点C是⊙O上异于点A的一点,且PC=PA.
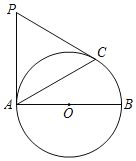
(1)求证:PC是⊙O的切线;
(2)若∠BAC=30°,AB=6,求∠P的度数及PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是G,过点B作BE⊥CG,垂足为E,且在AD上,BE交PC于点F,那么下列选项正确的是( )

①BP=BF;②如图1,若点E是AD的中点,那么△AEB≌△DEC;③当AD=25,且AE<DE时,则DE=16;④在③的条件下,可得sin∠PCB=![]() ;⑤当BP=9时,BEEF=108.
;⑤当BP=9时,BEEF=108.
A.①②③④B.①②④⑤C.①②③⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
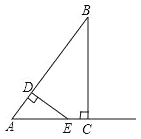
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=___________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,西藏日喀则市谢通门县发生了
日,西藏日喀则市谢通门县发生了![]() 级地震,某校九年班、九年二班两班的班长交流了为地震灾区捐款的情况:
级地震,某校九年班、九年二班两班的班长交流了为地震灾区捐款的情况:
(1)九年一班班长说:“我们班捐款总额为![]() 元,我们班人数比你们班多
元,我们班人数比你们班多![]() 人”.
人”.
(2)九年二班班长说:“我们班捐款总额也为![]() 元,我们班人均捐款比你们班人均捐款多
元,我们班人均捐款比你们班人均捐款多![]() ”.
”.
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将一块含有
中,将一块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
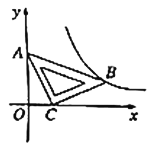
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
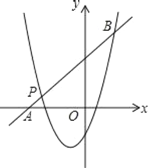
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值,
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,若点B与点M(﹣4,6)关于抛物线对称轴对称,求一次函数的表达式.
(3)根据函数图象直接写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com