
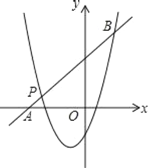
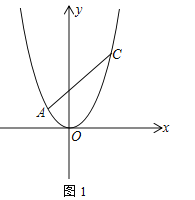
����Ŀ����֪���κ���y1��x2+mx+n��ͼ����P����3��1�����Գ����Ǿ�������1��0����ƽ����y���ֱ�ߣ�
��1����m��n��ֵ��
��2����ͼ��һ�κ���y2��kx+b��ͼ����P����x���ཻ�ڵ�A������κ�����ͼ���ཻ����һ��B������B���M����4��6�����������߶Գ���Գƣ���һ�κ����ı���ʽ��
��3�����ݺ���ͼ��ֱ��д��y1��y2ʱx��ȡֵ��Χ��
���𰸡���1��2��![]() ����2��y��x+4����3��x����3��x��2.
����2��y��x+4����3��x����3��x��2.
��������
��1������P��-3��1��������κ�������ʽ�ó�3m��n��8��Ȼ����ݶԳ�����㣨-1��0���ó��Գ���Ϊx=-1���ݴ����m��ֵ��Ȼ���һ�����n��ֵ���ɣ�
��2������һ�κ���������P����3��1�����ó�1����3k+b���ҵ�B���M����4��6������x����1�Գƣ�����B��2��6��������6��2k+b��������k��b��ֵ���ɣ�
��3��y1��y2����˵�� y1�ĺ���ͼ����y2����ͼ���Ϸ����ݴ˸���ͼ��ֱ��д����Χ����.
��1���ɶ��κ���������P����3��1����
��1��9��3m+n��
��3m��n��8��
�֡߶Գ����Ǿ�������1��0����ƽ����y���ֱ�ߣ�
��Գ���Ϊx����1��
�ੁ![]() ����1��
����1��
��m��2��
��n����2��
��2����һ�κ���������P����3��1����
��1����3k+b��
�ߵ�B���M����4��6������x����1�Գƣ�
��B��2��6����
��6��2k+b��
��k��1��b��4��
��һ�κ�������ʽΪy��x+4��
��3����ͼ���֪��x����3��x��2ʱ��y1��y2��


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2011���ݰ�˳��16��4�֣���ͼ����Rt��ABC�У���C=90����BC=6cm��AC=8cm����ͼ����ʾ��������BCD��BD�۵���ʹ��C����AB�ߵ�C���㣬��ô��ADC��������� ��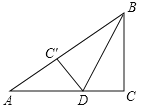
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��λҪ��һ�����Ϊ48 m2��С�ֿ⣬С�ֿ���һ�߿�ǽ(ǽ��10m)��������ǽƽ�е�һ�߿�һ����1 m���ţ�������Χ��19 m��ľ�壬��С�ֿ�ij������
(ע�⣺�ֿ⿿ǽ����һ�߲��ܳ���ǽ��)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���ص����һ���Ƕȵķ���������ڲ����ǿ��������������£�С��ķ��и߶�y��m�������ķ���ʱ��x��s��������κ�����ϵ��y��x�ļ����Ӧֵ�����ʾ��


��1����y����x�ĺ�������ʽ����Ҫ��дx��ȡֵ��Χ����
��2���ʣ�С��ķ��и߶��ܷ�ﵽ20.5m����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в�Ҷר��������ijƷ�Ʋ�Ҷ�������Ϊÿǧ�� 240 Ԫ����ÿǧ�� 400 Ԫ���ۣ�ƽ��ÿ�ܿ��۳� 200 ǧ�ˣ����������г����鷢�֣�����ÿ���� 10 Ԫ����ƽ��ÿ�ܵ������������� 40 ǧ�ˣ�����ר������������Ʒ�Ʋ�ҶҪ��ƽ��ÿ�ܻ��� 41600 Ԫ����ش�
��1��ÿǧ�˲�ҶӦ���۶���Ԫ��
��2����ƽ��ÿ�ܻ������������£�Ϊ�����������ڹ˿ͣ�Ӯ���г����õ�Ӧ��ԭ�ۼ۵� ���۳��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȥ��ɹ��ٰ�2018���ݹ������������Ļ��ڣ�������ȫ��ɭ������ʾ���С���ij����A��B��C��D��E������������ο�ϲ����һ�������ijС������������ڼ�ȥ��������������Σ�ֻѡһ������������������һ���������ͳ�ƣ����������ͳ�ƽ������������������������ͳ��ͼ��
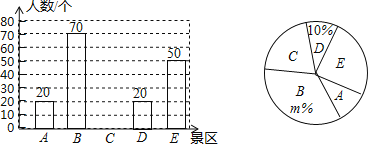
��1����С�������������������б����鵽���������� ���ˣ�![]() �� ��������ȫ����ͳ��ͼ��
�� ��������ȫ����ͳ��ͼ��
��2������С���о���1200�ˣ��Թ���ȥB�����εľ���Լ�ж����ˣ�
��3��С��ͬѧ��ȥ��E�����Σ�����ڼ�ƻ��븸ĸ��A��B��C��D�ĸ������У���ѡ����ȥ���Σ���ѡ��A��C���������ĸ��ʣ���Ҫ����״ͼ���б�����ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
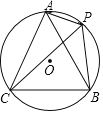
����Ŀ����ͼ��A��P��B��C�ǡ�O�ϵ��ĸ��㣬��APC����CPB��60�㣮
��1����֤��PA+PB��PC��
��2����BC��![]() ����P���ӻ�AB��һ���㣨����A��B����PA��PB�ǹ���x��һԪ���η���x2��mx+n��0����������m�����ֵ��
����P���ӻ�AB��һ���㣨����A��B����PA��PB�ǹ���x��һԪ���η���x2��mx+n��0����������m�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() �Ƿ���
�Ƿ���![]() ����������
����������![]() ������
������![]() ��ֱ��
��ֱ��![]() ��������ֻ��һ��������
��������ֻ��һ��������
��1����![]() ��
��![]() ��������ꣻ
��������ꣻ
��2����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
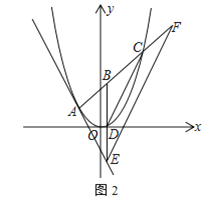
��3����ͼ2����![]() ���߶�
���߶�![]() �ϵĶ��㣬������
�ϵĶ��㣬������![]() ��
��![]() ���ƽ����
���ƽ����![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �����������ཻ�ڵ�
�����������ཻ�ڵ�![]() ������
������![]() ��
��![]() ��ƽ����
��ƽ����![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з����У�û��ʵ�������ǣ�������
A.2x+3��0B.x2��1��0C.![]() D.x2+x+1��0
D.x2+x+1��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com